アルゴリズム

実用日本語表現辞典

algorithm

別表記：アルゴリズム

「algorithm」とは・「algorithm」の意味

「algorithm」とは、問題を解決するための手順や計算方法を指す言葉である。コンピューターサイエンスや数学の分野でよく使われ、特にプログラミングにおいては、効率的なアルゴリズムが重要視される。アルゴリズムは、入力データを受け取り、一連の手順に従って処理を行い、最終的には出力データを生成する。

「algorithm」の発音・読み方

「algorithm」の発音は、IPA表記では /ˈælɡəˌrɪðəm/ であり、カタカナ表記では「アルゴリズム」となる。日本人が発音するカタカナ英語では「アルゴリズム」と読む。

「algorithm」の定義を英語で解説

An algorithm is a step-by-step procedure or set of instructions for solving a problem or accomplishing a task, especially in the fields of mathematics and computer science. Algorithms are often used in programming to process input data and generate output data in an efficient and accurate manner.

「algorithm」の類語

「algorithm」の類語には、以下のような言葉がある。

Procedure

「procedure」は、特定の目的を達成するための一連の手順や操作を指す。アルゴリズムと似ているが、より一般的な用途に使用される。

Method

「method」は、問題を解決するための手法やアプローチを指す。アルゴリズムと同様に、手順や計算方法を示すことがある。

「algorithm」に関連する用語・表現

Sorting algorithm

「sorting algorithm」は、データを特定の順序で並べ替えるためのアルゴリズムを指す。例えば、バブルソートやクイックソートなどがある。

Search algorithm

「search algorithm」は、データ構造から特定の要素を見つけ出すためのアルゴリズムを指す。例えば、線形探索や二分探索などがある。

「algorithm」の例文

1. The algorithm processes the input data and generates the output data.（アルゴリズムは入力データを処理し、出力データを生成する。） 2. He developed a new algorithm for solving the problem.（彼はその問題を解決するための新しいアルゴリズムを開発した。） 3. The efficiency of an algorithm is an important factor in programming.（アルゴリズムの効率はプログラミングにおいて重要な要素である。） 4. The sorting algorithm arranged the data in ascending order.（ソートアルゴリズムはデータを昇順に並べ替えた。） 5. The search algorithm found the target element in the data structure.（探索アルゴリズムはデータ構造から目的の要素を見つけ出した。） 6. The algorithm's complexity affects its performance.（アルゴリズムの複雑さはその性能に影響する。） 7. The programmer optimized the algorithm to reduce processing time.（プログラマーは処理時間を短縮するためにアルゴリズムを最適化した。） 8. The algorithm was tested on various data sets to ensure its accuracy.（アルゴリズムの正確性を確認するために、さまざまなデータセットでテストが行われた。） 9. The algorithm is designed to handle large amounts of data efficiently.（アルゴリズムは大量のデータを効率的に処理するように設計されている。） 10. The algorithm is based on a mathematical model.（アルゴリズムは数学的モデルに基づいている。）

（2023年7月10日更新）

デジタル大辞泉

アルゴリズム【algorithm】

読み方：あるごりずむ

ある特定の問題を解いたり、課題を解決したりするための計算手順や処理手順のこと。これを図式化したものがフローチャートであり、コンピューターで処理するための具体的な手順を記述したものがプログラムである。イランの数学者・天文学者、アル＝フワーリズミーにちなむ。

OR事典

アルゴリズム

読み方：あるごりずむ
【英】：algorithm

概要

その実行が必ず有限ステップで停止する有限個の機械的操作の列のこと. ここで, 機械的操作とは, 計算機の基本命令と考えて良い. ORにおいては, 定式化した問題に対し具体的に解を求めて現実に適用する必要があるので, 問題の解を得る効率の良いアルゴリズムを求めることは非常に重要である. アルゴリズムの代表的な設計法としては, 貪欲法(greedy), 2分探索, 動的計画, 分割統治等がある.

詳説

　アルゴリズム (algorithm) とは, その実行が必ず有限ステップで停止する有限個の機械的操作の列のことであり, 算法とも訳される.ここで, 機械的操作とは, 計算機の基本命令の列と考えて良い. この名称は, 9世紀のアラビアの代数学者, フワーリズミー (al-Khwarizmi) に由来する.数学の研究においては, 問題に対して解を構成する手順を求める接近法と, 解の存在を証明する接近法とが典型的であるが, 前者の, 解を求める手順のうち有限ステップで停止するものがアルゴリズムである. ユークリッド(Euclid) の互除法, 定規とコンパスによる作図, 高次方程式の解法等, 古くよりアルゴリズムを求める研究がなされてきた. その中で, アルゴリズムの概念を厳密に定義する必要性が, 1900年に提唱されたヒルベルト(D. Hilbert) の第10問題, すなわち, 不定不等式の有理整数解の存在を判定するアルゴリズムを求める問題以来, 次第に明確に意識されるようになり, 1930年代に至ってチューリング (A. M. Turing), チャーチ (A. Church), クリーネ (S. C. Kleene) によってそれぞれ異なった計算モデルを用いてアルゴリズムの厳密な定義がなされた. それらは, 等価であることが知られている. 特に, チューリングによりそれを解くアルゴリズムが存在しない問題があること (チューリング機械の停止問題, halting problem for Turing machines) が示されたことの意義は大きい.

　アルゴリズムの設計法は, 1940年代の電子計算機の出現とともに精力的に研究されてきた. 巡回セールスマン問題 (traveling salesman problem) 等, 原理的に有限ステップでは解けるが, 現実的な時間で解くアルゴリズムを作るのが困難な問題があることが知られるにつれ, 次第に計算の複雑さ (computational complexity) への認識が高まってきた. 一般に, 実行時間が入力サイズの多項式時間 (polynomial time) 以下のアルゴリズムを効率の良いアルゴリズムという. 1971年にクック (S. A. Cook) によりNP困難性 (NP-hardness, 計算の複雑さ参照) の概念が導入され, それ以来, カープ (R. Karp) を始め多くの研究者によって, 巡回セールスマン問題等, 組合せ最適化問題 (combinatorial optimizationproblem) を含む幾多の問題がNP困難であることが証明されてきた. あるNP困難な問題に対する多項式時間のアルゴリズムがあれば, 従来多項式時間のアルゴリズムを作るのが困難と思われてきた多くの問題に対しても多項式時間アルゴリズムが構成できる.しかしながら, それはほとんどありえないことから, NP困難な問題に対して多項式時間アルゴリズムは存在しないと信じられている.

　与えられた問題に対して効率の良いアルゴリズムを開発するには,

・問題の構造に対する深い洞察

・アルゴリズム設計技法の知識

が必要である.

　代表的なアルゴリズム設計技法としては以下のものが知られている.

・貪欲アルゴリズム (greedy, 欲張り法ともいう) : 解の構成要素を, 効果のあるものから順に選択していく.

　例: 最小木問題 (minimum spanning tree) に対するクラスカル (J. B. Kruskal Jr.) のアルゴリズム, その他, 近似アルゴリズム (approximation algorithm) としても良く用いられる.

・2分探索 (binary search): 予めソートされた列中で, ある要素を探す. 中央の要素と比較し, それよりも大きいか, 小さいかを調べ, ソート列中のどちら側にあるかを知る. 一回の反復毎に要素数が半分以下になるので, 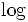(ソート列中の要素数) 回の比較で求まる.

　例: 辞書中での単語の検索.

・分割統治(divide and conquer): 解くべき問題を小規模な部分問題に分割して解き, 部分問題の解を統合することで全体の解を得ようとする方法. これは, 逐次のみならず並列アルゴリズムの設計においても基本的方法である.

・動的計画 (dynamic programming):「最適方策(optimal policy) は, それまでの決定がどのようであろうとも, それ以降も最適な決定を下さなければならない. (R. Bellman)」という, 最適性の原理 (principles of optimality) に基づく. アルゴリズム的観点から見ると, 一度計算した結果を記憶しておくことで冗長な再計算を避ける方法である. 最短路問題 (shortest path problem) に対する各種アルゴリズム等, グラフ・ネットワーク問題 (graph and network problems), および, 組合せ最適化問題において多くの応用例がある.

　問題が良い構造をもつと効率の良いアルゴリズムを設計することが可能となる. 特に, 貪欲アルゴリズムがうまく適用できる問題の構造については, マトロイド (matroid) の項目を, その他, グラフ・ネットワークの構造を持つ問題で効率の良いアルゴリズムが存在するものについては, グラフ・ネットワーク, グラフの連結度 (connectivity), ネットワークフロー問題 (network flow problem), マッチング問題 (matching problems) 等の項目を, また, 組合せ最適化問題について, その他, 劣モジュラ最適化 (submodular optimization), 離散凸解析 (discrete convexanalysis) 等の項目を参照されたい. また, データ構造 (data structure) を工夫することで効率の良いアルゴリズムを設計できる場合が多い.

　なお, アルゴリズムの実行時にデータが次々に入力され, 実行前には入力されるデータが未知であるアルゴリズムをオンラインアルゴリズム (online algorithm) という. オンラインアルゴリズムのいくつかの例が [1] にある. また, これまでは, 逐次かつ決定的アルゴリズムを論じてきたが, 実行に確率的動作を導入した確率アルゴリズム (probabilistic algorithm, または, ramdomized algorithm), 複数のプロセッサ上での並列アルゴリズム (parallel algorithm), および, 分散環境下での複数の計算機間に跨る計算に関する分散アルゴリズム (distributed algorithm) については, それぞれの用語解説, 及び, 並列アルゴリズムについては, [5, 9, 15, 16] を, 分散アルゴリズムについては, [10, 14, 19] を参照されたい. 文献[3] は, 連立1次方程式の解法, 逆行列の計算から始め, 非線形最適化 (nonlinear optimization), ネットワーク最適化 (networkoptimization) 等に関連した多様な並列, ないし, 分散アルゴリズムを扱っており, OR関係者にとって便利である. なお, 紙数の関係で本中項目では離散的対象に関する厳密に解を求めるアルゴリズムに話題を限ったが, 線形計画 (linear programming), 非線形計画 (nonlinear programming) 等, 各種数理計画に関するアルゴリズムについては, それぞれ該当する項目を参照されたい. また, NP困難な問題に対して良い実行可能解 (feasible solution) を現実的に求める近似アルゴリズムやその枠組であるメタヒューリスティックス (metaheurisitics) についても, それぞれ該当する項目を参照されたい.

---

参考文献

[1] A. V. Aho, J. E. Hopcroft and J. D. Ullman, The Design and Analysis of Computer Algorithms, Addison-Wesley, 1974; 野崎昭弘, 野下浩平共訳,『アルゴリズムの設計と解析I, II』, サイエンス社, 1977.

[2] 浅野孝夫, 今井浩, 『計算とアルゴリズム-計算機の科学-』, オーム社, 1986.

[3] D. P. Bertsekas, J. Tsitsiklis, Parallel and Distributed Computation, Prentice-Hall, 1989.

[4] T. H. Cormen, C. E. Leiserson, R. L. Rivest, Introduction to Algorithms, MIT Press, 1990; 浅野哲夫, 岩野和生, 梅尾博司, 山下雅史, 和田幸一訳,『アルゴリズムイントロダクション』, 第1-3巻, 近代科学社, 1995.

[5] A. Gibbons, W. Rytter, Efficient Parallel Algorithms, Cambridge University Press, 1988.

[6] 平田富夫,『アルゴリズムとデータ構造』, 森北出版, 1990.

[7] 茨木俊秀,『アルゴリズムとデータ構造』, 昭晃堂, 1989.

[8] 石畑清,『アルゴリズムとデータ構造』, 岩波書店, 1989.

[9] J. Jáá, An Introduction to Parallel Algorithms, Addison-Wesley, 1992.

[10] 亀田恒彦, 山下雅史,『分散アルゴリズム』, 近代科学社, 1994.

[11] D. E. Knuth, The Art of Computer Programming, Vol.I, Addison-Wesley, 1973; 広瀬健訳,『基本算法 / 基礎概念』, サイエンス社, 1978, および, 米田信夫, 筧捷彦訳, 『基本算法 / 情報構造』, サイエンス社, 1978.

[12] D. E. Knuth, The Art of Computer Programming, Vol.II, Addison-Wesley, 1981; 渋谷正昭訳,『準数値算法 / 乱数』, サイエンス社, 1981, および, 中川圭介訳, 『準数値算法 / 算術演算』, サイエンス社, 1986.

[13] Jan van Leeuwen ed., Handbook of Theoretical Computer Science Vol.A: Algorithms and Complexity, Elsevier Science B. V., 1990; 廣瀬健, 野崎昭弘, 小林孝次郎監訳,『コンピュータ基礎理論ハンドブックI, アルゴリズムと複雑さ』, 丸善, 1994.

[14] N. A. Lynch, Distributed Algorithms, Morgan Kaufmann, 1996.

[15] 宮野悟,『並列アルゴリズム』, 近代科学社, 1993.

[16] F. P. Preparata著, 上林弥彦, 岡部寿男, 浜口清治, 武永康彦編・訳,『プレパラータ先生の超並列計算講義』, 共立出版, 1996.

[17] R. Sedwick, Algorithms, 2nd ed., Addison-Wesley, 1988; 野下浩平, 星守, 佐藤創, 田口東共訳,『アルゴリズム第1巻=基礎・整列』, 近代科学社, 1990,『アルゴリズム第2巻=探索・文字列・計算幾何』, 近代科学社, 1992, および,『アルゴリズム第3巻=グラフ・数理・トピックス』, 近代科学社, 1993.

[18] 島内剛一, 有澤誠, 野下浩平, 浜田穂積, 伏見正則編,『アルゴリズム辞典』, 共立出版, 1994.

[19] G. Tel, Introduction to Distributed Algorithms, Cambridge University Press, 1994.

「OR事典」の他の用語

組合せ最適化：

AVL木  NP困難  TDI性  アルゴリズム  オンラインアルゴリズム  クラスMAX SNP  クラスNC

健康関連用語辞典

アルゴリズム

問題を解決するための手順や手続きを模式化したものです。

ウィキペディア

アルゴリズム

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2023/10/08 13:49 UTC 版)

アルゴリズム（英: algorithm）とは、解が定まっている「計算可能」問題に対して、その解を正しく求める手続きをさす。あるいはそれを形式的に表現したもの。

ウィキペディア小見出し辞書

アルゴリズム（木構造の場合）

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2015/11/08 04:34 UTC 版)

「深さ制限探索」の記事における「アルゴリズム（木構造の場合）」の解説

探索の始点となるノードを決定し、探索すべき深さの上限を決定する。 現在のノードが目標とする状態かどうか調べる。目標状態の場合: 探索成功。終了する。 現在のノードが探索すべき深さの範囲内にあるか調べる。範囲内の場合: ノードを展開し、深さ制限探索を再帰的に呼び出し、ステップ2に戻る。 探索失敗 木構造ではなく一般のグラフの場合、訪問済みのノードかどうかを管理すべき。ただし、深さ優先探索とは異なり、閉路があっても、無限ループに陥ることはない。また、訪問済みのノードを管理するとメモリ不足に陥る場合は、諦めるか、量を制限するかなどをする。

Wiktionary日本語版（日本語カテゴリ）

アルゴリズム

出典:『Wiktionary』 (2021/08/11 13:06 UTC 版)

語源

• 英語: algorithm

名詞

アルゴリズム

1. (数学) 問題を解くための手順。算法。
2. (プログラミング) コンピュータに処理を行わせるための手順。コンピュータが解釈できる形式で記したものをプログラムという。

発音^(?)

ア↗ルゴリ↘ズム

Weblio日本語例文用例辞書

「アルゴリズム」の例文・使い方・用例・文例

• 毎日大量の株を売買していることから、アルゴリズム取引のユーザーの大半を大手機関投資家が占めている。
• マーティンが発明したアルゴリズムは、株価の変動によってオプション価格がどれくらい変化するかを予測することができる。
• 数字の平方根を探すために、アルゴリズム用の擬似コードを書きなさい。
• あなたの平均を探すアルゴリズムをAとする。
• このソフトウエアはギブスサンプリングのアルゴリズムによりマルコフ連鎖モンテカルロ法の計算を行います。
• アルゴリズムの、アルゴリズムに関する、または、アルゴリズムの特徴がある
• リストを分類するアルゴリズム
• 共通の語幹への語形を減少するために屈折語尾と派生語尾を取り除くためのアルゴリズム
• 微積分学の問題の解決に近似するためのアルゴリズムを研究する数学の部門
• 代数的表現式に類似した命令文を持つアルゴリズム言語
• アルゴリズムを表すために設計された人工言語
• プログラミング言語で、コンピュータプログラムをアルゴリズムとして記述するのに使う
• 意図した結果を得ることに対する間違ったアルゴリズム、または方法の選択から生じるエラー
• 大きな既存のデータベースでのパターンと相関関係を発見するために高度なデータ検索能力と統計アルゴリズムを用いるデータ処理
• コンピューターグラフィックスで,Zバッファアルゴリズムという図形処理の手順
• ワーノック型アルゴリズムという,人間の視覚情報処理の手続きをコンピューターグラフィックス向けに一般化した手順