計算の複雑さ
【英】：computational complexity
概要
「計算の複雑さ」とは, その計算が必要とする計算資源の量を, 入力の長さに対する関数としてとらえるものである. 計算のモデルとしては, チューリング機械やRAMのモデルが使われ, 資源としては計算時間と計算に必要な領域が評価される. 一般には入力によって計算に必要な資源は変化するので, 入力の長さに関して最悪の場合を考える. 微妙な議論をしている場合以外は, 関数の多項式倍程度の差は無視する場合が多い.
詳説
「計算の複雑さ」とは，その計算が必要とする資源の量を，入力の長さに対する関数としてとらえるものである．計算のモデルとしては，チューリングマシンモデルが使われ，資源としては計算時間と計算に必要な領域が評価される．入力によって計算に必要な資源は変化するので，通常入力の長さに関して最悪の場合を考える．微妙な議論をしている場合以外は，関数の多項式倍程度の差は無視する場合が多い．こうした観点から言えば，現在世の中で利用されているフォン・ノイマン型の計算機はすべてチューリングマシンモデルで模倣することができる．また現実的に手に負える問題とは，多項式時間アルゴリズムで解ける問題だけと考えられている．
計算の複雑さの理論でもっとも有名な未解決問題は，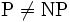
予想である．これはクラス
に属する問題がすべて多項式時間で解けるかどうか，という問題に対する予想である．NP困難な問題は数多く知られており，その中には実用上，重要な問題も含まれている (文献 [1] に詳細なリストがある)．多くの研究者は，NP困難な問題は多項式時間では解くことはできないであろう，と予想している．つまりこうした計算の複雑さの理論の枠組みによれば，ある問題がNP困難であることを示す，ということは，すなわちその問題が「手に負えない」問題であることを示した，ということであった．
しかし一方ではこうした従来の枠組みによって「手に負えない」とされた問題を，なんとかして現実的な観点から解決できないか，というアプローチもいくつか行われてきた．代表的なものとしては，確率的なアルゴリズムと，近似アルゴリズムとがあげられる．
確率的なアルゴリズムとは，計算機の基本的な機能としてコイントスを付加するアプローチである．コイントスを許したチューリングマシンモデル (確率チューリングマシンモデル) を導入し，正解を出力する確率によって問題のクラスを定義する．例えば一方向エラーを許した多項式時間の確率チューリングマシンによって判定できる問題はクラスRに属する．与えられた数が合成数かどうかを判定する問題が，クラスRに属することはよく知られている．こうしたアルゴリズムについては，文献 [6] が詳しい．
近似アルゴリズムとは，厳密な解ではなく，近似解を得られればよい，というスタンスに立つものである．近似解とは，通常は厳密な解に対する相対誤差が正定数で抑えられるものを言う場合が多い (問題によっては相対誤差でなかったり，正定数ではなく関数であったりする場合もある)．相対誤差が正定数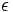
で抑えられる解を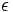近似の解と呼ぶ．近似アルゴリズムでは正定数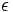に対して「入力の長さ」と「
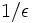」の多項式時間で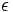近似の解を求めることができるかどうか，という基準で「手に負えない」問題であるかどうかを決める．同じNP困難な問題であっても，こうした観点からは違った性質をもつものがあることがわかっている. つまりNP困難な問題であっても，与えられた任意の正定数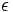に対して，上記の意味での多項式時間で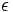近似の解を求めることができるものがあり，一方では
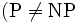の仮定のもとでは
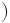多項式時間で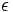近似の解を求めることのできるような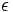の大きさに限界がある問題も知られている．後者の問題の属するクラスの一つとしてクラスMAX SNPが知られている．つまりMAX SNP困難な問題は，厳密解だけではなく，よい近似解を求めることですら「手に負えない」問題である，ということになる．ここで注意すべき点は，こうした意味で「手に負えない」問題であっても，ある程度の近似アルゴリズムが知られているものがある，ということである．つまりいくらでもよい近似率を達成するのは困難ではあるが，特定の近似率を実現するのであれば，なんとかなる問題もある．しかしこうした問題の近似率をどこまで小さくできるか，という問題は一般には非常に難しい．こうした問題や最近の結果については，文献[3][8]が詳しい．
計算の複雑さの理論では，こうした「手に負えるかどうか」という観点とは別の切口から問題の複雑さを研究する分野もある．例えば「与えられた問題を並列に効率よく解くことができるかどうか」という観点も実用上，重要な意味を持つ．ある問題に対して，並列化が効果的かどうかは，その問題がどの程度「並列性」を有しているかによる．並列性を有する問題のクラスの一つがクラスNCである．このクラスに属する問題は，プロセッサを増やせば，その分だけ効率よく問題を解くことができる．多項式時間アルゴリズムを持つ問題の中には，このクラスに属さないであろう，と強く予想されている問題もある．こうした問題はプロセッサ数を増やしても計算の高速化には限界がある．こうした並列計算に関する問題については，文献 [2] のリストが詳しい．
なお本項目全般については，文献 [5, 7] が詳しい．文献 [4] は非常に幅広い話題を網羅した著名なハンドブックである．
[1] M. R. Garey and D. S. Johnson, Computers and Intractability: A Guide to the Theory of NP-Completeness}, Freeman, San Francisco,1979.
[2] R. Greenlaw, H. J. Hoover and W. L. Ruzzo, Limits to Parallel Computation, Oxford University Press, 1995.
[3] D. S. Hochbaum (eds.) Approximation Algorithms for NP-hard Problems, PWS Publishing Company, 1995.
[4] J. van Leeuwen (eds.) Handbook of Theoretical Computer Science, Elsevier Science Publishers, 1990.
[5] 守屋悦朗,『チューリングマシンと計算量の理論』, 培風館, 1997.
[6] R. Motwani and P. Raghavan Randomized Algorithms, Cabbridge, 1995.
[7] C.H. Papadimitriou Computational Complexity, Addison-Wesley Publishing Company, 1994.
[8] V. V. Vazirani, Approximation Algorithms, Springer, 2001. 浅野孝夫訳, 『近似アルゴリズム』, シュプリンガー・フェアラーク, 2002.
計算の複雑さ
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2022/03/02 07:32 UTC 版)
計算複雑性理論は、問題を解決するために必要なリソース（通常は時間またはメモリ ）の量が、入力のサイズに対してどのように増加するかを論じる。 古典的な計算複雑性理論の拡張として、 量子計算複雑性理論は、物理的な量子コンピュータの構築の難しさやデコヒーレンスとノイズの影響を必ずしも考慮せずに、理論的な汎用量子コンピュータに何ができるかを議論する。量子情報は古典的な情報を一般化したものであるため 、 量子コンピュータはあらゆる古典的なアルゴリズムをシミュレートできる 。 複雑度クラスBQP （有界誤差量子多項式時間）は、 汎用量子コンピュータによって多項式時間で解くことができる決定問題のクラスである。重要な古典的複雑性クラスの階層に関連付けらる P ⊆ B P P ⊆ B Q P ⊆ P S P A C E {\displaystyle P\subseteq BPP\subseteq BQP\subseteq PSPACE} 。これらの包含関係が厳密かどうか（等号が成立しないかどうか）はどれも未解決の問題である。 古典的なコンピューティングでは計算できないことを証明する難しさは、量子優越性を示す上での一般的な課題である。 白黒をはっきりつける決定問題とは異なり、サンプリング問題は、ある確率分布からのサンプルを求める。 任意の量子回路の出力から効率的にサンプリングできる古典的なアルゴリズムがある場合、 多項式階層は第3レベルに折りたたまれるが、これはほとんどあり得ないと考えられてる。 ボソンサンプリングは、より具体的な提案であり、その古典的な難しさは、複雑なエントリを持つ大きな行列のパーマネントを計算する難しさに依存する。これは、#P完全な問題である。この結論に到達するために使用された議論は、IQPサンプリングにも拡張され、そこでは問題の平均と最悪のケースの複雑さは同じであるという推測のみが必要となる。
※この「計算の複雑さ」の解説は、「量子超越性」の解説の一部です。
「計算の複雑さ」を含む「量子超越性」の記事については、「量子超越性」の概要を参照ください。
- 計算の複雑さのページへのリンク
