くみあわせさいてきか‐もんだい〔くみあはせサイテキクワモンダイ〕【組(み)合(わ)せ最適化問題】
組合せ最適化問題
【英】:combinatorial optimization problem
概要
離散最適化問題のうち, 解集合の定義が組合せ的条件によるものをいう. 多くの組合せ的条件は, 変数の整数性を含む形式で表現できるため, 整数計画問題とほぼ同義的に用いられることも多い. 一般に問題のサイズが大きくなるにつれ, 対象とすべき解の数が爆発的に増加するため, 有効な時間で最適解を得るのが困難な問題が多く含まれている. そのため, 近似的な解を有効な時間や精度で求める研究も盛んである.
詳説
ある計画を遂行するとき, 様々な条件を満足させながら, 最適な順序を決めたり, 複数の選択肢からいくつかを選んだり, 仕事と機械とを割り当て (一般化割当問題) たり, 施設の配置場所を決め (施設配置問題) たりする問題は現実の中でもよく当面する. これらの問題, あるいは論理代数学にみられる充足可能性問題 (satisfability problem) などのように, 解集合が順列, 組合せなどで表される離散最適化問題 (discrete optimization problem) を総称して組合せ最適化問題 (combinatorial optimization problem) という.
ほとんどの組合せ最適化問題は, 変数に整数性を含む形式で数学的に表現できるため, 整数計画問題と明確な区別はできない. 慣例的には, 巡回セールスマン問題 (traveling salesman problem), ナップサック問題 (knapsack problem), 集合被覆問題 (set covering problem)などのように,問題や解の構造に何等かの特徴のある離散最適化問題を, より一般的な整数計画問題と区別して, 組合せ最適化問題と呼ぶこともある.
組合せ最適化問題の難しさは, 一般に問題のサイズが大きくなるにつれ, 解集合を構成する要素の数が組合せ的に増加 (組合せ的爆発) することにある. したがって, たとえ有限ではあっても, すべての解を列挙して最適な解を得ることは事実上不可能となる. また, それらの多くがNP困難なクラスに属するため,単純なアルゴリズムや貪欲的な解法だけでは, 最悪の場合,最適とはかけ離れた (問題のサイズの増大に従って急速に悪くなるような) 解が得られることさえもある.
組合せ最適化問題を厳密に解くアプローチとしては,それらが (0-1) 整数計画問題に定式化できることから, そこで研究・開発されている解法のほとんど全てが, 組合せ最適化問題にも適用可能であるため, 一般的な整数計画問題を解くパッケージなどを利用するのも一法ではある. しかしながら, 組合せ最適化問題は,制約式の表現形式そのものが組合せ的に増大してしまうこともあるため, 単にソフトウェア任せでは, 問題の入力時点ですでに行き詰まってしまうことも少なくない.
例えば 都市の巡回セールスマン問題の場合,
都市の巡回セールスマン問題の場合,  をグラフの点集合とし,
をグラフの点集合とし, 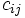 を枝
を枝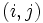 の重み,
の重み,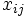 を枝
を枝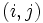 が解に含まれるとき1, そうでないとき0の値をとる0-1変数とするとき, 次のように定式化することができる.
が解に含まれるとき1, そうでないとき0の値をとる0-1変数とするとき, 次のように定式化することができる.
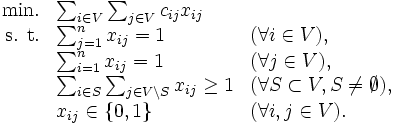
この定式化では, 変数の数は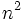 であり, 制約式の1, 2番目は各
であり, 制約式の1, 2番目は各 本で割当問題と同じ形をしているが, 部分巡回路除去制約と呼ばれている第3番目の制約は, 式の数が組合せ的に増大するため, 一般的な整数計画問題のパッケージを使うことは難しい. もちろん, 1つの問題に対する定式化の方法は一意ではなく, 巡回セールスマン問題を2次割当問題 (quadratic assignment problem) や 3部グラフにおける割当問題に帰着して定式化すれば, パッケージの利用は可能になるが, それによって解きやすくなることは期待できない.
本で割当問題と同じ形をしているが, 部分巡回路除去制約と呼ばれている第3番目の制約は, 式の数が組合せ的に増大するため, 一般的な整数計画問題のパッケージを使うことは難しい. もちろん, 1つの問題に対する定式化の方法は一意ではなく, 巡回セールスマン問題を2次割当問題 (quadratic assignment problem) や 3部グラフにおける割当問題に帰着して定式化すれば, パッケージの利用は可能になるが, それによって解きやすくなることは期待できない.
定式化における規模の増大を克服する試みもなされている. たとえば, 板取り問題 (cutting-stock problem) は, 変数の数が非常に多くなる形で定式化できるが, 列生成法によって必要な変数 (取り出しパターン) を生成しながら解くことで成功をおさめている. また, 巡回セールスマン問題のように制約式が非常に多くなる問題については, 必要な制約を随時加え, 解領域を次第に狭くしていきながら解く 切除平面法 (cutting plane method) が適用できる.
切除平面法は, 組合せ最適化問題を研究する上で, 歴史的にも理論的にも重要な位置を占めている. この方法の基本的な考え方は, まず問題の整数条件を連続緩和した問題を考える. このとき, さらに制約式の一部を除去してもよい. 例えば, 巡回セールスマン問題の場合, 第3番目の制約式を除いて緩和した問題は割当問題と等価になる. この緩和問題を解くと, 一般に元問題にとっては実行不可能な解が得られる. ここで, その解は切除するが, 元問題の実行可能解は切除しないような制約を生成し, それらを逐次加えていきながら, 連続緩和問題を解き続ける. その結果, 最初に出た実行可能解が最適解となる.
切除平面法の正当性は理論的に裏付けられているが, 単独利用だけでは収束性や計算機の精度などにおいて難があり, 1970-80年代にはより実用的な分枝限定法に軍配があがっていた. しかし近年では分枝限定法の中に切除平面法を組み込む手法 (分枝切除法) が様々な問題で成功をおさめ, 再び注目を浴びつつある.
分枝限定法 (branch-and-bound method) は, 分割統治法の一種であり, そのままの問題では規模が大きすぎて解きにくいものを, 変数などを固定することにより解領域を解ける程度にまで小さな問題 (子問題) に分割し, 各子問題, あるいはその緩和問題を解いて得られる情報をまとめて, 元の問題の最適解を得ようという考えに基づいている.
分枝限定法の基本的な枠組みは以下のように記述できる. ただし, ここでは最小化問題について説明しており, 上界値というのは, 最適値以上であることが分かっている値で, 通常近似解法などで得られる値をさす. また, 下界値というのは, 最適値以下であることが分かっている値で, 緩和問題などを解いて得られる値のことをいう. 最大化問題の場合は, 上界値・下界値の意味が逆転することに注意されたい. 以下では, 未探査の子問題の集合を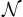 とする.
とする.
分枝限定法は基本的に列挙法であり, 最悪の場合を考えれば全ての解を列挙してしまうこともあり得るが, 多くの場合極めて効果的に働き, 無駄な列挙を削除することで, かなり大規模な問題であっても最適解を得ることに成功している.
無駄な列挙を削除できる場合というのは, 緩和問題が実行不可能のとき(step3), 緩和問題の解が実行可能のとき(step4), 緩和問題の最適値が上界値と等しいか悪い (大きい) とき (step5) であるが,その中でも特にstep5の果たす役割は非常に大きい. これをうまく働かせるためには, より大きな下界値を得ることと, 近似解法などを用いてよりよい上界値を得ること (step1) が必要不可欠である. その他にも, 探索する子問題の選択 (step2) や子問題の分割法 (step6) も重要な役割を果たす.
以下では, 下界値を改善する代表的な方法としてラグランジュ緩和法 (Lagrangian relaxation method) と切除平面法について説明する.
ラグランジュ緩和は, 問題の緩和のため, 除去した制約にラグランジュ乗数というスカラーを掛けて目的関数に加えて作成する. ラグランジュ緩和の作り方は, どの制約を目的関数に組込むかでいく通りも考えられるが, 一般的に残った制約式が解きやすい問題となるものを選ぶ. 例えば巡回セールスマン問題の場合には, 第3番目の制約をラグランジュ緩和すると, 次の割当問題となり, この最適値は巡回セールスマン問題の下界値を与える. ただし, 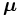 はラグランジュ乗数ベクトル, 各要素は
はラグランジュ乗数ベクトル, 各要素は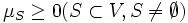 である. 等式制約をラグランジュ緩和するときには, ラグランジュ乗数に符号の制約は付かない.
である. 等式制約をラグランジュ緩和するときには, ラグランジュ乗数に符号の制約は付かない.
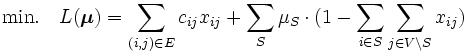
このとき, できるだけ大きな下界値を得るような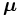 を定めることが大切であり, それをラグランジュ最適化問題 (ラグランジュ双対問題) という. つまり,
を定めることが大切であり, それをラグランジュ最適化問題 (ラグランジュ双対問題) という. つまり, 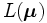 の最適値を
の最適値を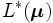 とするとき,
とするとき,
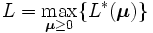
と表現される問題である. この問題を解くために, 微分不可能な区分線形関数における非線型最適化手法のひとつである 劣勾配法 (subgradient method) と呼ばれる逐次反復法が用いられることが多い. 劣勾配法による反復は, かなり少ない回数で打ち切っても, 十分良い下界値が求まることが様々な問題において報告されている.
効果的な下界値を算出するもう1つの方法として, 切除平面法を分枝限定法に組込む分枝切除法 (branch-and-cut method)が, 大規模な組合せ最適化問題を効果的に解く方法として注目を浴びつつある. これは, 切除平面法が解領域を徐々に狭くしていくことから, よりよい緩和問題を解いていると捉えるものである. 特に元の問題にとっての実行不可能な解をできるだけ大きく切り落とすような, (極大面) カットとよばれる不等式の様々な生成法が研究されている.
組合せ最適化問題の厳密解法において, 分枝限定法は布の縦糸のようなもので, それに横糸であるラグランジュ緩和法, 劣勾配法, 切除平面法,近似解法などを絡めることにより, 優れた解法が開発されている. 分枝限定法は, 非凸領域をもつ数理計画問題や, 大域最適化問題などの解法としても注目を浴びつつある.
組合せ最適化問題に関する文献は, 理論的なもの, 実験的なもの, 実例的なもの, 近似解法など様々な視点から, それぞれ膨大な数の優れた論文や著書がある. 近年, ハンドブック的な書籍 [2, 3] 等が出ており,邦訳されたもの [4, 5] もある. 特に [1] は, 文献の書評集であり, 適切な文献を探すのに有用である.
[1] M. Dell'Amico, F. Maffioli and S. Martello, eds., Annotated Bibliographies in Combinatorial Optimization, John Wiley & Sons, 1997.
[2] D.-Z. Du and P.M. Pardalos, eds.,Handbook of Combinatorial Optimization, 3 vols., Kluwer, 1998.
[3] R.L. Graham, M. Grötschel and L. Lovász, eds.,Handbook of Combinatorics, 2 vols., North-Holland, 1995.
[4] B. Korte and J. Vygen, Combinatorial Optimization: Theory and Algorithms, Springer, 2002. 浅野孝夫, 平田富夫, 小野孝男, 浅野泰仁訳, 『組み合わせ最適化 - 理論とアルゴリズム』, シュプリンガー・フェアラーク, 2005.
[5] G.L. Nemhauser, A.H.G. Rinnooy Kan and M.J.Todd, eds.,Optimization, North-Holland, 1989. 伊理正夫, 今野浩, 刀根薫監訳, 『最適化ハンドブック』, 朝倉書店, 1995.
組合せ最適化
(組合せ最適化問題 から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/03/10 02:06 UTC 版)

|
この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 (2018年12月)
|
組合せ最適化(くみあわせさいてきか、英: combinatorial optimization、組み合わせ最適化、または組み合せ最適化とも表記される)は、応用数学や情報工学での組合せ論の最適化問題である。オペレーションズリサーチ、アルゴリズム理論、計算複雑性理論と関連していて、人工知能、数学、およびソフトウェア工学などの交差する位置にある。組合せ最適化では、厳密解が簡単に求まる場合もあれば、そうでない場合もある。厳密解を求めるのが難しいと思われる問題を解くために、その問題の解空間を探索する場合もあり、そのためのアルゴリズムでは、効率的に探索するために解空間を狭めたりすることもある。
非形式的定義
組合せ最適化は、最適化問題の中でも最適解の集合が離散的であるか、離散的なものに減らすことができるものであり、その目的は最も良い解決法を見つけることである。
解が二値ベクトルの場合は0-1最適化問題(英: 0-1 optimization problem)とも言われる。
形式的定義
組合せ最適化問題のインスタンスは、 
| 一般 | |
|---|---|
| 微分可能 |
| 凸最小化 | |||||||
|---|---|---|---|---|---|---|---|
| 線形 および 二次 |
|
| 系列範例 (Paradigms) |
|||||
|---|---|---|---|---|---|
| グラフ理論 |
|
||||
| ネットワークフロー (最大流問題) |
- 組合せ最適化問題のページへのリンク
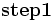
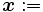
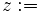
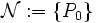 (元
(元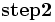
 ならば
ならば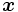 が
が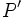 を
を とする.
とする.
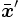 ,
, 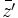 (この値は
(この値は
 なら
なら ,
, 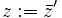 として
として
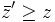 ならば子
ならば子