ナップザック‐もんだい【ナップザック問題】
ナップサック問題
【英】:knapsack problem
重さが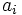 の物品
の物品 をナップサックに詰めるとき, 重量制限
をナップサックに詰めるとき, 重量制限 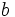 の下で価値
の下で価値 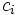 の総和が最大になるものを選ぶという次の整数計画問題.
の総和が最大になるものを選ぶという次の整数計画問題.
| 目的関数 | 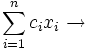 最大化 最大化 |
| 制約条件 | 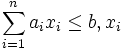 :非負整数 :非負整数 |
NP困難であるが, 実際には大規模な問題でも最適に解くことができる. 板取り問題などの部分問題などにも広く利用されている.
ナップサック問題
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/03/14 06:02 UTC 版)

|
この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 (2016年9月)
|

ナップサック問題(ナップサックもんだい、英: Knapsack problem)は、計算複雑性理論における計算の難しさの議論の対象となる問題の一つで、n 種類の品物(各々、価値 vi、重量 wi)が与えられたとき、重量の合計が W を超えない範囲で品物のいくつかをナップサックに入れて、その入れた品物の価値の合計を最大化するには入れる品物の組み合わせをどのように選べばよいか」という整数計画問題である。同じ種類の品物を1つまでしか入れられない場合(xi ∊ {0, 1})や、同じ品物をいくつでも入れてよい場合(xi は0以上の整数)など、いくつかのバリエーションが存在する。
決定問題としてのナップサック問題は、「W, vi, wi のほかに価値の合計の目標 V が与えられたとき、重量の合計が W 以内でナップサック内の品物の価値の合計が V 以上になるような品物の選び方が存在するか」を判定することである。 全ての品物について vi = wi である場合は、部分和問題と等価であるため、ナップサック問題は部分和問題の一般化である。ナップサック問題は、(部分和問題もそうであるが)NP困難と呼ばれる問題のクラスに属する。なお、部分和問題は同時にNP完全(NPかつNP困難)と呼ばれるクラスにも属する。
解法として、動的計画法を用いた擬多項式時間アルゴリズムや FPTAS の存在が知られており、実用的にはほぼ最適な解が得られる。
定義

- ナップサック問題のページへのリンク
