データ構造

OR事典

データ構造

読み方：でーたこうぞう
【英】：data structure

概要

与えられたデータを, 計算の高速化のために構造をもたせて記憶する手法の総称. 目的に合わせ, あるいくつかの機能を, 高速, あるいは省メモリで行えるよう設計される. 例えば, ある言葉を 個の言葉の辞書データから検索するとき, 通常の配列では, 最悪で挿入・削除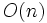に , 検索に 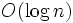か, 挿入と削除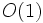に , 検索に 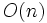の時間を要する. 二分探索木というデータ構造は, これらの機能を 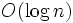時間で行い, 使用メモリは 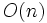である.

詳説

　データ構造とは, 与えられたデータに対して, そのデータを使った計算の高速化, そのデータを記憶するために必要な領域の減少等の目的で, データに構造を持たせ, データに対する操作の効率化を行う手法の総称である. あるいくつかの機能を, データの記憶形式と, その形式のデータを操作するアルゴリズムにより実現する.

　通常のコンピューター言語では, データを蓄える手法として配列かリスト, またはその両方が用意されている. 配列は指定した位置にあるデータに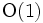時間でアクセスでき, リストは与えられたデータを並べて記憶し, 隣のデータに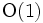時間でアクセスできる. リストは配列により実現可能だが, リストで配列は実現できない.

　配列やリストは最も単純なデータ構造である. ここで両者を使ったデータ構造の性能の違いを見てみよう. 例として 行 列の行列 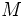を保持し, 他の行列との掛け算を行うためのデータ構造を考える. 通常の配列を使用して行列を記憶する場合 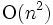のメモリが必要であるが, もし 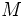の非零要素の数 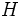が小さい場合, 非零要素を連結してリストで持つことにより, 記憶容量を 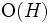まで減少させることができる. 行列の掛け算は非零要素に関する部分だけ計算を行えばよいので, 計算時間も2つの行列の非零要素の数の積に比例する. しかし, リストは一要素を記憶するのに必要なメモリが配列に比べて大きいので, 非零要素が多い場合はリストのほうが遅く, メモリも多くなる.

　次に, 個の用語の辞書データを保持し, その中から与えられた用語を検索するためのデータ構造を考える. データに変更がないときは, 用語を辞書順で並べて記憶すれば, 二分探索により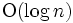時間で1つの用語が検索できる. しかし, 辞書データの中の用語を削除する・新しい用語を追加する, という操作が必要な場合には, 通常平均的に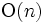の時間を要する. 辞書順に並べるかわりに, 二分探索木 (AVL木, 2-3木など) というデータ構造を用いれば, 使用メモリは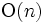のままで, これらの操作の実行時間を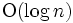まで減らすことができる. このようにデータの動的な変化に対しても効率が良く操作が行えるよう設計されたデータ構造を動的データ構造という. 辞書データを扱う他の効率の良いデータ構造としてはハッシュ表が知られている.

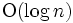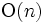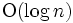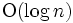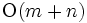　動的データ構造の中で最も基礎的なものとしてはヒープが挙げられる. 基本的なヒープは, 個の要素の中の最小値を得る・要素の追加・削除するという操作を, 1回あたり時間で実行し, またメモリ使用量もである. 応用も広く, プリム法 (最小木問題のアルゴリズム), 最少費用フロー問題 (最小費用流問題) のアルゴリズムなどで使用される. また, 改良版の Fヒープ (フィボナッチヒープ) は, 最短路問題を解くアルゴリズムで使われている. その他, 個の区間の集合を保持し, 質問点を含む区間を列挙する, 区間の挿入・削除を行う, などの操作を1回あたり 時間で行う区分木, 大きさ の木構造のグラフに対し, 合併・分割・変形・ある頂点の子孫数を求める, など多くの操作を時間で行う動的木, 集合の合併と要素の探索を高速化し, 回の合併と 回の探索の合計時間がほぼ となる集合ユニオン・ファインド木, 動的に変化する有向グラフの強連結性を保持し, 回の枝の挿入・削除を 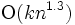で行うデータ構造[7], など数多くのものが考案されている. 文字列やグラフを扱う離散アルゴリズムの多くは, これらの基礎的なデータ構造に手を加えたものを使用することにより高速化されている. また, アルゴリズムの動作記録を変換して保持し, パラメーターの変更による計算結果の変化を出力するデータ構造は動的計画, 組み合わせ最適化問題の感度分析などに応用が広い.

　データ構造, 特に動的データ構造は, 計算幾何学における発展が著しい. 幾何的なデータはデータの量に対して構造が複雑なものが多い. 例えば, 平面上の 点の集合に対し, 距離が 以下の2点を枝でつないだグラフ(幾何グラフ)を考える. このグラフは 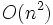本の枝を含む可能性があるが, このグラフを記憶するには点集合だけ記憶すれば十分である. つまり, メモリや計算時間を省略するためには, 点集合のデータから必要な枝の情報を得るための構造が必要となる. また, 枝の交差など, グラフ的な情報からは導けないものもあり, それらの情報を効率的に得るためにもデータ構造はかかせない. 幾何的なデータ構造としては, 平面上の点集合の凸包を保持し, 点の追加・消去に対し新しい凸包を 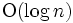時間で求めるもの, 次元の 点集合に対し, 質問点から近い順に点を1個あたり平均 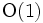時間で出力する 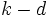木, 質問領域の中に含まれる点を1個あたり 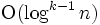で出力するレンジサーチ木 [8], 平面をいくつかの領域に分割する 本の線分の集合が与えられたとき, 質問点がどの領域に含まれるかを 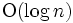時間で答える領域探索などが挙げられる. その他に, 線分の集合に対し, ある点から見える点, すなわち2点をつなぐ線分が他の線分と交差しないような点集合を保持するデータ構造など, 交差, 領域に関してさまざまなデータ構造が考案されている.

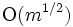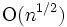　前述の幾何的なデータ構造は, 幾何的な対象を扱う計算幾何学のアルゴリズムで多く使われている. 多角形の三角形分割の線形時間アルゴリズムなども高度な技術を用いてデータ構造を活用しているが, しかしその反面複雑になりすぎ, 現実的ではないという欠点がある. また, 個々のアルゴリズムで使用するデータ構造がそのアルゴリズムに特化した, 一般性のないアルゴリズムとデータ構造も少なくない. それゆえ, 最近では簡素化も視野に入れた研究が進んでいる. スパーシフィケイション [6] もその一つであり, 動的データ構造高速化の一般化した技術を提供している. スパーシフィケーションにより, 頂点 枝を持つ無向グラフの最小全張木を保持するデータ構造は, 1回の枝の追加・削除・重みの変化に対する計算時間が, から に高速化される. 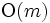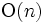また同様にグラフの二部グラフ性の判定, 二連結性の判定, 頂点連結性の判定なども, 一回の操作の計算時間が から に高速化される.

　最後に参考文献を挙げる. 動的木などグラフ的なデータ構造は [3], [4], [5] 等に詳しい. また, 幾何的データ構造については [1], [2] 等が詳しい.

---

参考文献

[1] F. P. Preparata and M. L. Shamos, "Computational Geometry - An Introduction," Springer-Verlag, 1985. 浅野孝夫, 浅野哲夫 訳,『計算幾何学入門』, 総研出版, 1992.

[2] 今井浩, 今井圭子,『計算幾何学』, 共立出版, 1994.

[3] T. H. Cormen, C. E. Leiserson and R. L. Rivest, "Introduction To Algorithms," The MIT Press, 1990. 浅野哲夫, 岩間和生, 梅尾博司, 山下雅史, 和田幸一 訳,『アルゴリズムイントロダクション 1,2,3巻』, 近代科学, 1995.

[4] 浅野孝夫,『情報の構造 上, 下』, 日本評論社, 1994.

[5] 茨木俊秀,『アルゴリズムとデータ構造』, 昭晃堂, 1989.

[6] D. Eppstein, Z. Galil, G. F. Italiano, A. Nissenzweig "Sparsification - A Technique for Speeding up Dynamic Graph Algorithms," FOCS, 33, 1992

[7] S. Khanna, R. Motwani and R. H. Wilson, "On Certificates and Lookahead in Dynamic Graph Problems," SODA, 1995

[8] D. E. Willard "New Data Structures for Orthogonal Range Queries," SIAM Journal on Computing, 14 (1985), 232-253.

「OR事典」の他の用語

組合せ最適化：

クラスR  グラフ彩色問題  グレブナー基底  データ構造  ナップサック問題  ネットワークフロー問題  ハッシュ表

ウィキペディア

データ構造

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2021/12/09 05:28 UTC 版)

データ構造（データこうぞう、英: data structure）とは、コンピュータプログラミングにおけるデータの集まりへの、アクセスと修正を容易にした構成・管理・保存の形式である。データ構造は、一定の関係性を持たせたデータ型のコレクションであり、データ値に適用するための関数や手続きも内包されることがある。データの代数的構造とも言われる。

ウィキペディア小見出し辞書

データ構造

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2018/07/22 02:07 UTC 版)

「ハッシュライフ」の記事における「データ構造」の解説

一般に、ライフゲームの（理論上の）フィールドは無限に広い格子である。扱いやすさなどのために、多くの場合、その格子点に縦横に整数で付番し、原点すなわち (0, 0) の近くに有限個の「生存」セルによるパターンがあるものとし、残りの無限の部分を無限個の非生存のセルとする。以上は理論的な観点からの話だが、実装では、生存しているセルがある付近を十分にカバーできる情報があれば良い。 ハッシュライフでは、1辺が2の冪乗個のセルの正方形の領域を、縦横それぞれ2等分する四分木構造の再帰でフィールドを表現する。この時、その範囲内のフィールドの状態にもとづくハッシュ値をキーにしたハッシュテーブルを併用し、全く同じ状態のフィールドであれば、四分木構造における部分木を共有する（すなわち、実際には木ではなくDAGとなっている）。このようなハッシュ（ハッシュテーブル）を利用した効率化を図るものであることから、その名がある。 一般的なライフゲームのアプリケーションソフトのエンジンとして利用するには、全盤面の1世代後を得る手続きも実装する必要もあるが、少々煩雑な部分があるのでここでは省略する。以下で述べる高速化についても、概要のみとする。 ここで、木の深さ0で一辺が1セルとする。規則的で再帰的な四分木構造により、深さ1では一辺が2セルの正方形、深さ2では一辺が4セル……というようにして、深さkの木は一辺が2k個のセルからなる22k個のセルの正方形をあらわしている（前述のように具体的にはDAGで実装する）。周辺との干渉があるから、「その領域全体の未来の状態」のメモ化は不可能である。1辺が4セルの時、その中央の2x2の領域の1世代先の状態については確定的なのでメモ化できる。そして、8x8の領域に対しては中心4x4の領域の2世代先の状態、16x16の領域に対しては中心8x8の領域の4世代先の状態というように、倍々で、より未来の世代のメモ化が可能であり、また、効率的に計算することもできるというのが急所である。一般に、木の深さkで、中心にある2k-1x2k-1個のセルの正方形の領域の2k-2世代先をメモ化できる。この「メモ」の範囲とその未来の世代は、ライフゲームの「光速」によって、その世代における結果は確定的であることから、うまく機能するということが言える。ハッシュライフの著しい利点として、このメモ化の利用により、例えば動作が数万世代を超えるような巨大なパターンについて、何世代もスキップさせつつ、その後の結果のみを迅速に得ることができる。

データ構造

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2020/05/21 05:56 UTC 版)

「隣接行列」の記事における「データ構造」の解説

隣接行列は、グラフを操作するためのコンピュータプログラムにおけるグラフの表現のためのデータ構造として使うことができる。この応用のためにも使われる主な代替データ構造は隣接リストである。 隣接行列中の各成分は1ビットしか必要としないため、隣接行列は非常にコンパクトなやり方で表すことができ、有向グラフを表わすためにはわずか|V |2/8バイト、無向グラフを表わすためには（パック三角形式を用い、行列の下部三角部分のみを格納することによって）わずか約 |V |2/16しか占めない。わずかにより簡潔な表現も可能であるものの、この方法は全てのn頂点グラフを表わすために必要な最小ビット数の情報理論的下界に近付く。テキストファイルにグラフを格納するためには、全てのバイトがテキスト文字であることを（例えばBase64表現を使うことによって）保証するためにバイト毎により少ないビットした使うことができない。無駄な空間を避けることに加えて、このコンパクトさは参照の局所性を促す。しかしながら、大きな疎グラフ（英語版）では、隣接リストのほうが必要とする格納空間が小さい。これは、隣接リストは存在「しない」辺を表わすためのいかなる空間も無駄にしないためである。 隣接行列の別形式（しかし、より大きな空間量を必要とする）は行列の個々の要素中の数を（辺が存在する時は）辺オブジェクトへのポインタあるいは（辺が存在しない時は）ヌルポインタで置き換える。また、辺の重みを隣接行列の要素中に直接格納することも可能である。 空間のトレードオフに加えて、異なるデータ構造は異なる操作をも容易にする。隣接リスト中の任意の頂点に隣接する全ての頂点を探すことはリストを読むのと同じぐらい単純であり、隣の数の比例した時間がかかる。隣接行列を使うと、代わりに全行をスキャンしなければならず、これはグラフ全体の中の頂点の数に比例したより長い時間がかかる。一方、任意の2つの頂点間に辺が存在するかどうかを調べるのは隣接行列を使うと瞬時に決定することができるのに対して、隣接リストを使うと2つの頂点の最小次数に比例した時間を要する。

データ構造

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2021/08/06 09:44 UTC 版)

「データモデル」の記事における「データ構造」の解説

データ構造は、データを効率的に使えるようコンピュータに格納する1つの方法である。それは、データの数学的かつ論理的な概念の1つの組織化である。しばしば、注意深く選ばれたデータ構造が、最も効率的なアルゴリズムの利用を可能とする。データ構造の選択はしばしば、抽象データ型の選択から始まる。 データ･モデルは、与えられたドメイン内のデータの構造を、そのドメイン自身の基盤をなす構造をほのめかすことによって、記述する。これは、そのドメインに専用の人工言語の専用文法を、実際に規定することを意味する。データモデルは、企業が保持しようと望む情報、その情報の属性、およびそれらのエンティティ間の関連と（時には暗示的に）それらの属性間の関連についての、エンティティのクラス（ものの種類）を表現する。そのモデルは、どのようにデータがコンピュータ・システム内で表現されるかにかかわらず、いくらかの広がりへのデータの組織を記述する。 データモデルによって表現されるエンティティは、触知可能なエンティティであり得るが、そのような具体的エンティティ・クラスを含むモデルは、時間を越えて変化する傾向がある。堅牢なデータモデルは、しばしばそのようなエンティティの抽象概念を認識する。たとえば、1つのデータモデルが、ある組織と関連する全ての人間を表す、「人材」と呼ばれるエンティティ・クラスを含むかもしれない。そのような抽象エンティティクラスは、それらの人材によって演じられる特定の役割を識別する「ベンダー」または「従業員」と呼ばれるより、一般に適切である。 配列 ハッシュテーブル 連結リスト スタック構造

データ構造

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2021/05/23 05:10 UTC 版)

「GNU Octave」の記事における「データ構造」の解説

Octaveではユーザーがデータ構造をある程度定義できる。たとえばスカラー、行列、文字列の変数を持つ構造体を以下のようにして定義できる。 octave:1> x.a = 1; x.b = [1, 2; 3, 4]; x.c = "string";octave:2> x.aans = 1octave:3> x.bans = 1 2 3 4octave:4> x.cans = stringoctave:5> xx ={ a = 1 b = 1 2 3 4 c = string}

データ構造

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2021/07/13 15:44 UTC 版)

「FIFO」の記事における「データ構造」の解説

キューに格納されたデータの処理方法のひとつである。キュー上の各要素はキューのデータ構造内に格納される。FIFOのキューでは、最初に格納されたデータが、(後で)最初に取出されると同時に削除される。入出力（格納と取出し）は常にその順番で行われる。同義語としてLILO（Last In Last Out）がある。これはキューの一般的な動作である。これの対称として、先入れ後出し（後入れ先出し）の順序があり、スタックまたはLIFOを参照されたい。 典型的なデータ構造は次のようになる。 struct fifo_node { fifo_node *next; value_type value; }; class fifo { fifo_node *front; fifo_node *back; fifo_node dequeue(void) { fifo_node *tmp = front; front = front->next; return tmp; } queue(value) { fifo_node *tempNode = new fifo_node; tempNode->value = value; back->next = tempNode; back = tempNode; } } この例では、queue(value) で valueがキューに格納され、dequeue() でキューの先頭のデータを取り出すようになっている。

データ構造

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2022/05/19 14:30 UTC 版)

「Icon」の記事における「データ構造」の解説

Iconはリスト、テーブル型（連想配列）、集合、レコード型（構造体）など、多数のデータ構造を提供している。例えばリストを得るには cat := ["muffins", "tabby", 2002, 8] などとすればよい。 ただし上記にないデータ構造も、配列、スタック、キューはリストとの区別が無いだけであり、文字列 は文字型の配列として扱うので、これらのデータ構造の機能をもっていないというわけではない。 またIconの変数は基本的にデータの型を宣言する必要が無いが、データ型が存在しないというわけではなく、型推論が行われているだけである。このため、上記のデータ構造を利用する場合は使用前に宣言を行う必要がある。この宣言は代入文の形で行われる、例えば連想配列の場合 t := table()t["abc"] := 1 となる。これは連想配列tを使用する前にt := table()によってtが連想配列であることを明記している。

データ構造

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2017/04/10 06:42 UTC 版)

「ビットプレーン」の記事における「データ構造」の解説

音声データの変位をPCM化したデータや、ビットマップ画像の輝度のデータの場合、元データの最上位ビットに相当するビットプレーンが全体のデータとしては最も重要であり、最下位ビットに対応するビットプレーンは最終的な音声や輝度への影響が最も少ない。（画像データであればガンマの考慮などが本来は必要だが、ここではそういったものは全て無視するとして）一般に、あるビットと比較して、そのひとつ下位のビットによる影響は 1/2 である。 例えば、8ビットの値 10110101（十進では181）をビットプレーンに分解すると次のようになる。 ビットプレーン値寄与累積7 1 1 * 2^7 = 128 128 6 0 0 * 2^6 =0 128 5 1 1 * 2^5 = 32 160 4 1 1 * 2^4 = 16 176 3 0 0 * 2^3 = 0 176 2 1 1 * 2^2 = 4 180 1 0 0 * 2^1 = 0 180 0 1 1 * 2^0 = 1 181 （ここではLSB側を0としたが、MSB側を0とする場合もある）

データ構造

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2020/11/04 14:58 UTC 版)

「Apple event」の記事における「データ構造」の解説

Apple eventには属性とパラメタという2種類の情報が格納される。属性はイベントの役割を記したものであり、パラメタはイベントで用いられるデータである。属性とパラメタはApple eventに複数格納でき、4バイトキャラクタのキーワードによって各項目が識別される。Apple eventの属性には最低限「対象プロセス」と「イベントクラス」と「イベントID」を特定する情報がなくてはならない。イベントクラスとはイベントの内容をおおまかに分類するものであり、イベントIDとはイベントクラスをさらに細かく分類するものである。Apple eventを言葉に例えるならば、対象プロセスは話しかける相手、イベントクラスとイベントIDは動詞に相当するもの、パラメタは名詞に相当するものと言える。 イベントクラスには基本的な処理を扱うコアイベントクラスが定義されており、アプリケーションは最低限、次のようなイベントIDに対応することが推奨されている（注：コアイベントクラスのイベントIDは下記のほかにもある）。 kAEOpenApplication ('oapp') - アプリケーションを起動する kAEQuitApplication ('quit') - アプリケーションを終了する kAEOpenDocuments ('odoc') - 書類を開く kAEPrintDocuments ('pdoc') - 書類を印刷する Apple eventによって扱われるデータは、すべてApple eventデスクリプタと呼ばれる構造に格納される。Apple eventデスクリプタには、データの種類を識別する「デスクリプタタイプ」と、データの本体が格納される。Apple eventデスクリプタに格納できるデータの種類は任意であるが、あらかじめ多くのデスクリプタタイプ（数値、文字列、ファイル参照、オブジェクト指定子など）が定義されているほか、Apple eventデスクリプタはリスト（配列）やレコード（4バイトキャラクタのキーワードによって項目が識別される連想配列）を格納したり、入れ子にもできる。プログラムで扱われるApple event（送信前のもの、受信したもの）も、レコード型のApple eventデスクリプタの派生型である。

データ構造

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2022/01/04 09:25 UTC 版)

「Pure Data」の記事における「データ構造」の解説

Pd の特筆すべき機能は、データ構造を視覚的に表現できることである。これには様々な応用が考えられ、作曲やイベントの順序付けから、視覚的な作品を作ったり、Pd 自体のGUIを拡張したりできる。 Pure Data（純粋なデータ）の名の通り、Pd のデータ構造は音楽データを静止画としても動画としても表現できる。C言語の構造体のように Pd のデータ構造は様々なデータで構成でき、データ構造の視覚化をデータ構造でパラメータ指定することで制御したり、Pd のパッチ内でのメッセージや音声信号を制御したりできる。Puckette は以下のように記している。 Pd はデータ構造とそのグラフィカルな外観を記述するために全く構造化されていない環境を提供するよう設計されている。根底にある考え方は、ユーザーが任意のデータを任意の見せ方で表示できるようにすることである。このため、Pd では C言語などとは全く異なる、データに形や色を与える視覚的なデータ構造を導入し、ユーザーがデータを視覚的に編集できるようにした。データは内部で編集することも、ファイルから読み込むことも、アルゴリズムによって生成することも、入力音声やデータを解析することで作成することもできる。— Miller Puckette、Pd Documentation Chapter 2 — 2.9. Data structures

データ構造

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2020/11/17 06:20 UTC 版)

「GLib」の記事における「データ構造」の解説

頻繁に利用されるデータ構造とそれに対する操作が定義されている。以下に主なものを列挙する。 メモリチャンク 双方向および片方向線形リスト 連想配列（ハッシュテーブル方式の実装） 可変長文字列 可変長配列 文字列チャンク（文字列のグループ） 動的配列 平衡2分探索木 N分木 quarks（文字列とユニークな整数識別子を対応付けるもの） keyed data lists（文字列や整数識別子でアクセス可能なデータ要素群） リレーションとタプル 構造体のキャッシュ

Weblio日本語例文用例辞書

「データ構造」の例文・使い方・用例・文例

• 木のような構造に配置され、いくつかの段階を持ったデータ構造
• プログラマが一揃いのプロシージャをそれぞれのデータ構造のタイプに関連付けられるようにするプログラミング言語