gruff
「gruff」の意味・「gruff」とは
英語の単語「gruff」は、日本語に訳すと「ぶっきらぼうな」「無愛想な」といった意味を持つ。人の態度や話し方に対して使われる形容詞である。例えば、人が他人に対してあまり感情を見せず、短く厳しい言葉で話すとき、その人の態度や話し方を「gruff」と表現することができる。「gruff」の発音・読み方
「gruff」の発音は、IPA表記では/grʌf/となる。IPAのカタカナ読みでは「グラフ」となる。日本人が発音するカタカナ英語では「グラフ」と読む。この単語は発音によって意味や品詞が変わる単語ではない。「gruff」の定義を英語で解説
英語の辞書で「gruff」を調べると、「(of a voice or manner) rough and low in pitch」という定義が見つかる。これは、「声や態度が荒く、低い音程である」という意味を表している。この定義からも、「gruff」が人の態度や話し方に対して使われる形容詞であることがわかる。「gruff」の類語
「gruff」の類語としては、「brusque」「curt」「blunt」などが挙げられる。これらの単語も同様に、人の態度や話し方が短く、直接的で、感情をあまり見せない様子を表す形容詞である。「gruff」に関連する用語・表現
「gruff」に関連する表現としては、「gruffly」がある。これは副詞形で、「ぶっきらぼうに」「無愛想に」という意味を持つ。また、「gruffness」は名詞形で、「ぶっきらぼうさ」「無愛想さ」を表す。「gruff」の例文
1. He has a gruff manner that can be off-putting.(彼は無愛想な態度を持っていて、それが人々を遠ざけることがある。)2. Her gruff voice was intimidating.(彼女のぶっきらぼうな声は威圧的だった。)
3. He answered in a gruff voice.(彼はぶっきらぼうな声で答えた。)
4. Despite his gruff exterior, he's really very kind.(彼のぶっきらぼうな外見に反して、彼は本当にとても親切だ。)
5. She was put off by his gruff manner.(彼の無愛想な態度に彼女は引いた。)
6. He spoke in a gruff voice.(彼はぶっきらぼうな声で話した。)
7. His gruff demeanor belies his warm heart.(彼のぶっきらぼうな態度は彼の温かい心を隠している。)
8. She responded gruffly to his question.(彼の質問に彼女はぶっきらぼうに答えた。)
9. His gruffness is just a facade.(彼のぶっきらぼうさはただの外面だ。)
10. Despite his gruff voice, his words were kind.(彼のぶっきらぼうな声にもかかわらず、彼の言葉は優しかった。)
グラフ【graph】
グラフ【Steffi Graf】
グラフ
研究結果の発表において論点を図解するために、グラフ表示 1ないし図示 1の手法を用いることがある。データは図 2、グラフ 2、統計図表 2、または地図 3によって示される。変数間の関係の図式的表示は、たとえばレキシスの図式(レキシス・ダイアグラム)(437参照)のように、図式(ダイアグラム) 4と呼ばれることが多い。一方の座標軸が対数的に、他方が等間隔に目盛られたグラフは片対数グラフ 5と呼ばれるが、そのようなグラフは対数グラフ 5と不正確ないい方で呼ばれることが多い。真の対数グラフ 6は両方の軸が対数的に目盛られたもので、両対数グラフ 6と呼ばれることもある。度数分布のグラフ表示には、階級度数を表示する点を直線で繋ぐことによって得られる度数多角形 7、階級間隔を底辺とする長方形の面積によって階級度数が表示される柱状図(ヒストグラム) 8、階級度数が棒の長さに比例する棒グラフ 9、累積度数分布を表す累積度数分布図(オージャイブ) 10などがある。
グラフ (QC七つ道具の)
【英】:graph
QC七つ道具の1つで, データを図に表し, データ全体の傾向を把握したり,変化の状態を明確にしたりするために用いられる. 折れ線グラフ, 棒グラフ,円グラフ, 帯グラフ, レーダーチャートなどがよく用いられる.
グラフ (グラフ理論の)
【英】:graph
概要
グラフは, 点の集合 , 枝の集合
, 枝の集合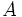 および各枝
および各枝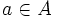 の始点と終点を指定する2つの写像
の始点と終点を指定する2つの写像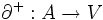 と
と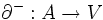 からなる複合概念であり, グラフ
からなる複合概念であり, グラフ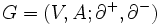 (あるいは
(あるいは 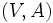 )のように記される. グラフは平面上に, 点を丸で, 枝を矢線で描き, 幾何学的に表現される. 枝
)のように記される. グラフは平面上に, 点を丸で, 枝を矢線で描き, 幾何学的に表現される. 枝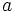 の矢線の始点が
の矢線の始点が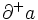 を, 終点が
を, 終点が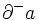 を表す. 枝の方向を考慮する場合を有向グラフ, 考慮しない場合を無向グラフと呼び区別する.
を表す. 枝の方向を考慮する場合を有向グラフ, 考慮しない場合を無向グラフと呼び区別する.
詳説
グラフ (graph)は,点の集合 ,枝の集合
,枝の集合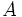 および各枝
および各枝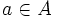 の始点と終点を指定する二つの写像
の始点と終点を指定する二つの写像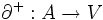 と
と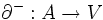 からなる複合概念であり,グラフ
からなる複合概念であり,グラフ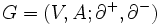 のように記される.また,しばしば
のように記される.また,しばしば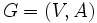 のように略記される.グラフは平面上に,点を丸で,枝を矢線で描き,幾何学的に表現される.枝
のように略記される.グラフは平面上に,点を丸で,枝を矢線で描き,幾何学的に表現される.枝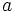 の矢線の始点が
の矢線の始点が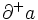 を,終点が
を,終点が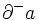 を表している.
を表している.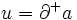 で
で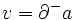 であるとき,枝
であるとき,枝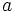 は点
は点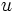 から点
から点 への枝といわれる.すべての2点
への枝といわれる.すべての2点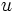 ,
,  に対して点
に対して点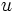 から点
から点 への枝が高々1本だけであるとき, 点
への枝が高々1本だけであるとき, 点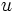 から点
から点 への枝があればそれを
への枝があればそれを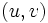 のように点の順序対で表現することも多い.これからも分かるようにグラフはその点集合上の2項関係を表すものであると考えることができる.様々なシステムの構造を捕らえるとき, それらのシステムの構成要素の間の2項関係を考えることはもっとも基本的であり, モデル化も容易である.枝
のように点の順序対で表現することも多い.これからも分かるようにグラフはその点集合上の2項関係を表すものであると考えることができる.様々なシステムの構造を捕らえるとき, それらのシステムの構成要素の間の2項関係を考えることはもっとも基本的であり, モデル化も容易である.枝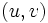 は
は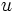 から
から へのものの流れ(の存在)を表現したり,
へのものの流れ(の存在)を表現したり, 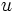 から
から への因果関係,通信ケーブルや道路などのリンクの存在などを表現したりする.日常的にも用いられる「・・・ネットワーク」や「・・・網」といわれるものはグラフ構造を持つものである.
への因果関係,通信ケーブルや道路などのリンクの存在などを表現したりする.日常的にも用いられる「・・・ネットワーク」や「・・・網」といわれるものはグラフ構造を持つものである.
取り扱う問題によっては, 各枝の始点と終点がどちらであるかを気にしない(すなわち対称な2項関係を考える)こともある.このようなとき,平面上の幾何学的表現では各枝を表現する矢線から矢印を取って,そのグラフを表現する.このようなグラフは無向グラフ (undirected graph) と呼ばれる.最初に定義した通常のグラフを無向グラフと対比して示したいとき, これを有向グラフ (directed graph あるいは digraph) という.グラフの用語については,日本語および英語の両方とも,必ずしも統一されていない.点は,頂点,節点とも呼ばれ,枝は,辺,弧,線などとも呼ばれる.英語では,点はvertex, node, 枝は edge, arc などがよく用いられる(枝に対し有向グラフでarc, 無向グラフでedgeを用いる流儀もある).グラフの枝(や点)にそれに付随する容量,長さ,費用などの属性を付与してグラフ中のものの流れなどを考える場合, これをネットワーク (network) と呼ぶ.
グラフ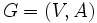 上の点
上の点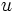 から点
から点 へ枝の向きは無視して接続する点と枝をたどって到達できるとき,たどる順に得られる点と枝の交互列を点
へ枝の向きは無視して接続する点と枝をたどって到達できるとき,たどる順に得られる点と枝の交互列を点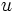 から点
から点 への道(あるいは路)(path) という.その道上の枝がたどる向きにすべて揃っているとき,そのような道を有向道(あるいは有向路)(directed path)という.道および有向道は,少なくとも1本の枝を含み, その始点と終点が一致するとき,閉路(closed path (cycle))および有向閉路(directed closed path (directed cycle))と呼ばれる.平面上に枝を交差させることなく幾何学的に表現することが可能なグラフを平面グラフ (planar graph) という.閉路を含まない連結なグラフを木 (tree)という.グラフ
への道(あるいは路)(path) という.その道上の枝がたどる向きにすべて揃っているとき,そのような道を有向道(あるいは有向路)(directed path)という.道および有向道は,少なくとも1本の枝を含み, その始点と終点が一致するとき,閉路(closed path (cycle))および有向閉路(directed closed path (directed cycle))と呼ばれる.平面上に枝を交差させることなく幾何学的に表現することが可能なグラフを平面グラフ (planar graph) という.閉路を含まない連結なグラフを木 (tree)という.グラフ の点集合
の点集合 のある2分割
のある2分割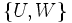 が存在して,各枝が
が存在して,各枝が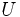 の点と
の点と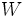 の点を結ぶとき,このグラフ
の点を結ぶとき,このグラフ を2部グラフ (bipartite graph) という.
を2部グラフ (bipartite graph) という.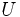 と
と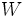 の点の数がそれぞれ
の点の数がそれぞれ と
と であって,
であって,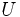 の各点と
の各点と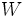 の各点を結ぶ枝が丁度1本存在するとき,この2部グラフを完全2部グラフと言い,
の各点を結ぶ枝が丁度1本存在するとき,この2部グラフを完全2部グラフと言い, 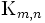 のように表す.グラフ
のように表す.グラフ が自己閉路(1本の枝からなる閉路)を含まず, そのすべての相異なる2点に対してそれらを結ぶ丁度1本の枝が存在するとき,このグラフを完全グラフ (complete graph)(あるいは完備グラフ)という.ここで,
が自己閉路(1本の枝からなる閉路)を含まず, そのすべての相異なる2点に対してそれらを結ぶ丁度1本の枝が存在するとき,このグラフを完全グラフ (complete graph)(あるいは完備グラフ)という.ここで, の点の数が
の点の数が であるとき,これを
であるとき,これを 点完全グラフと呼び,
点完全グラフと呼び, 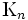 のように表す.
のように表す.
二つのグラフ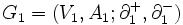 と
と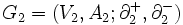 に対して, グラフ
に対して, グラフ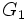 の点と枝の接続関係は保ったまま
の点と枝の接続関係は保ったまま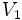 の各点の名前(ラベル)を変えて
の各点の名前(ラベル)を変えて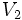 とし,同時に
とし,同時に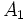 の各枝の名前(ラベル)を変えて
の各枝の名前(ラベル)を変えて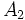 としてグラフ
としてグラフ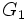 からグラフ
からグラフ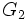 を得ることが可能であるとき, これらの二つのグラフは同形である (isomorphic)という.また,二つのグラフ
を得ることが可能であるとき, これらの二つのグラフは同形である (isomorphic)という.また,二つのグラフ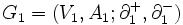 と
と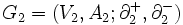 に対して,
に対して, 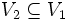 ,
, 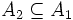 であり,
であり,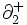 が
が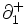 を,
を,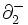 が
が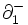 を,それぞれ,
を,それぞれ,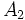 上に制限したものになっているとき, グラフ
上に制限したものになっているとき, グラフ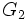 をグラフ
をグラフ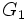 の部分グラフという.与えられたグラフ
の部分グラフという.与えられたグラフ の幾何学的表現から,いくつかの枝を消し,いくつかの孤立して残る点を消して得られる幾何学的表現に対応するグラフが元のグラフ
の幾何学的表現から,いくつかの枝を消し,いくつかの孤立して残る点を消して得られる幾何学的表現に対応するグラフが元のグラフ の部分グラフである.
の部分グラフである.
[1] C. Berge, Graphes et Hypergraphes, Dunod, 1970. 伊理正夫 他 訳,『グラフの理論, I~III』, サイエンス社,1976.
[2] J. A. Bondy and U. S. R. Murty, Graph Theory with Applications, North-Holland, 1976.
[3] R. Diestel, Graph Theory, 3rd ed., Springer, 2005. 根上生也,太田克弘 訳, 『グラフ理論』, シュプリンガー・フェアラーク東京,2000.
[4] F. Harary, Graph Theory, Addison-Wesley, 1969. 池田貞雄 訳,『グラフ理論』, 共立出版,1971.
| グラフ・ネットワーク: | TSP多面体 クラスカル法 クラスター分析 グラフ シュタイナー最小木 ダイクストラ法 ダルメジ・メンデルゾーン分解 |
グラフ
グラフ
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/07/03 03:36 UTC 版)
グラフ
graph
チャートも参照。
幾何学的表現
- 情報を二次元平面上に表したもの。
→詳細は「ダイアグラム」を参照
- グラフ理論の「グラフ」- 一般的な用語では「ネットワーク」などと呼ばれるものに感覚的には相似した、節点と枝(頂点と辺、などと呼ぶこともある)からなる構造。
- グラフ (データ構造) の記事では、データ構造としての観点からの上述のグラフについて述べている。
- グラフ (離散数学)
視覚的表現
- 数量の時間変化や大小関係、割合などを、視覚的に表現した図。統計グラフ。
→詳細は「統計図表」を参照
- 関数を特徴付ける集合で、曲線や曲面とみなせるものもある。
→詳細は「グラフ (関数)」を参照
- 写真や絵画など視覚的に表現された図案、またはそれを主とする雑誌。
→詳細は「グラフ誌」および「画報」を参照
Graf
関連項目
グラフ
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2016/04/11 07:26 UTC 版)
クラブのこと。
※この「グラフ」の解説は、「ゴニンカン」の解説の一部です。
「グラフ」を含む「ゴニンカン」の記事については、「ゴニンカン」の概要を参照ください。
グラフ
「グラフ」の例文・使い方・用例・文例
- 棒グラフ
- 折れ線グラフ
- 新しいパラグラフで書き出しなさい
- このグラフは若者による犯罪の急激な増加を示します
- 彼が下のグラフを見る
- 弊社がメカニカルクロノグラフモデル1機種を1月25日より全国で発売します
- 社外のグラフィッカーにデザインを発注する予定だ。
- 新しいコロナグラフがついに完成した。
- 多機能クロノグラフ
- 彼女はお気に入りの歌手のディスコグラフィーをダウンロードした。
- QC7つ道具は、特性要因図、チェックシート、ヒストグラム、散布図、パレート図、グラフ ・層別の7つがある。
- 消費者行動を分析する際は、アンケート調査によるサイコグラフィック変数も加味する必要がある。
- ペイオフダイアグラムでは戦略の採算性をグラフを用いて表す。
- 宗教や人種的背景は、いくつかの国に存在するが他の国には存在しないデモグラフィック変数の例である。
- 私の母はうつ病の疑いがあるので、光トポグラフィー検査を受けに行きます。
- 民族学者を育成し、民俗学研究を推進するため、ABC大学にエスノグラフィー・センターが設立された。
- 下記グラフは20代後半の女性の平均消費性向を示している。
- 「棒足」は上に高値を、下に安値を示している棒グラフのことである。
- 下記グラフは名目所得の推移を示している。
- 私は日本に滞在しながら、ファッションフォトグラファーの仕事をしています。
グラフと同じ種類の言葉
「グラフ」に関係したコラム
-
株式分析の出来高陰陽線とは、ローソク足の形によって出来高のグラフに色を分けて表示するテクニカル指標です。出来高陰陽線は、ローソク足が陰線の場合には、陰線の色と同じ色で出来高のグラフを描画します。例えば...
-
株式の株価チャートをエクセルで表示する方法を紹介します。まず、下の図のように、エクセルのシートのセルに、出来高、日付、始値、高値、安値、終値の列を作成します。次に、各列にデータを入力していきます。行の...
-
CFDで取引されるオレンジジュースの実体はオレンジ果汁を冷凍濃縮した状態のもので、Frozen Concentrate Orange Juice(FCOJ)、ICE US Frozen Concent...
FXのチャート分析ソフトMT4のGator Oscillatorの見方
FX(外国為替証拠金取引)のチャート分析ソフトMT4(Meta Trader 4)のGator Oscillatorの見方について解説します。Gator Oscillator(ゲーターオシレーター)は...
-
小麦は、米やトウモロコシと並んで世界の三大穀物として世界各国で消費されています。次の図は、小麦の生産量をグラフに表したものです(アメリカ合衆国農務省調べ)。EU27か国、中国、インド、アメリカ合衆国の...
FXのチャート分析ソフトMT4のMoving Average of Oscillatorの見方
FX(外国為替証拠金取引)のチャート分析ソフトMT4(Meta Trader 4)のMoving Average of Oscillatorの見方について解説します。Moving Average of...
- グラフのページへのリンク




