グラフ (QC七つ道具の)
【英】:graph
QC七つ道具の1つで, データを図に表し, データ全体の傾向を把握したり,変化の状態を明確にしたりするために用いられる. 折れ線グラフ, 棒グラフ,円グラフ, 帯グラフ, レーダーチャートなどがよく用いられる.
グラフ (グラフ理論の)
【英】:graph
概要
グラフは, 点の集合 , 枝の集合
, 枝の集合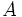 および各枝
および各枝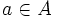 の始点と終点を指定する2つの写像
の始点と終点を指定する2つの写像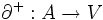 と
と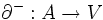 からなる複合概念であり, グラフ
からなる複合概念であり, グラフ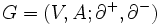 (あるいは
(あるいは 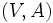 )のように記される. グラフは平面上に, 点を丸で, 枝を矢線で描き, 幾何学的に表現される. 枝
)のように記される. グラフは平面上に, 点を丸で, 枝を矢線で描き, 幾何学的に表現される. 枝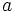 の矢線の始点が
の矢線の始点が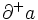 を, 終点が
を, 終点が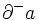 を表す. 枝の方向を考慮する場合を有向グラフ, 考慮しない場合を無向グラフと呼び区別する.
を表す. 枝の方向を考慮する場合を有向グラフ, 考慮しない場合を無向グラフと呼び区別する.
詳説
グラフ (graph)は,点の集合 ,枝の集合
,枝の集合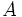 および各枝
および各枝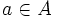 の始点と終点を指定する二つの写像
の始点と終点を指定する二つの写像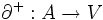 と
と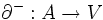 からなる複合概念であり,グラフ
からなる複合概念であり,グラフ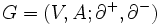 のように記される.また,しばしば
のように記される.また,しばしば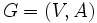 のように略記される.グラフは平面上に,点を丸で,枝を矢線で描き,幾何学的に表現される.枝
のように略記される.グラフは平面上に,点を丸で,枝を矢線で描き,幾何学的に表現される.枝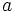 の矢線の始点が
の矢線の始点が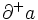 を,終点が
を,終点が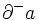 を表している.
を表している.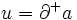 で
で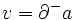 であるとき,枝
であるとき,枝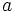 は点
は点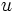 から点
から点 への枝といわれる.すべての2点
への枝といわれる.すべての2点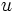 ,
,  に対して点
に対して点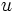 から点
から点 への枝が高々1本だけであるとき, 点
への枝が高々1本だけであるとき, 点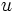 から点
から点 への枝があればそれを
への枝があればそれを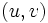 のように点の順序対で表現することも多い.これからも分かるようにグラフはその点集合上の2項関係を表すものであると考えることができる.様々なシステムの構造を捕らえるとき, それらのシステムの構成要素の間の2項関係を考えることはもっとも基本的であり, モデル化も容易である.枝
のように点の順序対で表現することも多い.これからも分かるようにグラフはその点集合上の2項関係を表すものであると考えることができる.様々なシステムの構造を捕らえるとき, それらのシステムの構成要素の間の2項関係を考えることはもっとも基本的であり, モデル化も容易である.枝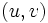 は
は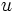 から
から へのものの流れ(の存在)を表現したり,
へのものの流れ(の存在)を表現したり, 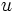 から
から への因果関係,通信ケーブルや道路などのリンクの存在などを表現したりする.日常的にも用いられる「・・・ネットワーク」や「・・・網」といわれるものはグラフ構造を持つものである.
への因果関係,通信ケーブルや道路などのリンクの存在などを表現したりする.日常的にも用いられる「・・・ネットワーク」や「・・・網」といわれるものはグラフ構造を持つものである.
取り扱う問題によっては, 各枝の始点と終点がどちらであるかを気にしない(すなわち対称な2項関係を考える)こともある.このようなとき,平面上の幾何学的表現では各枝を表現する矢線から矢印を取って,そのグラフを表現する.このようなグラフは無向グラフ (undirected graph) と呼ばれる.最初に定義した通常のグラフを無向グラフと対比して示したいとき, これを有向グラフ (directed graph あるいは digraph) という.グラフの用語については,日本語および英語の両方とも,必ずしも統一されていない.点は,頂点,節点とも呼ばれ,枝は,辺,弧,線などとも呼ばれる.英語では,点はvertex, node, 枝は edge, arc などがよく用いられる(枝に対し有向グラフでarc, 無向グラフでedgeを用いる流儀もある).グラフの枝(や点)にそれに付随する容量,長さ,費用などの属性を付与してグラフ中のものの流れなどを考える場合, これをネットワーク (network) と呼ぶ.
グラフ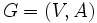 上の点
上の点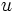 から点
から点 へ枝の向きは無視して接続する点と枝をたどって到達できるとき,たどる順に得られる点と枝の交互列を点
へ枝の向きは無視して接続する点と枝をたどって到達できるとき,たどる順に得られる点と枝の交互列を点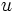 から点
から点 への道(あるいは路)(path) という.その道上の枝がたどる向きにすべて揃っているとき,そのような道を有向道(あるいは有向路)(directed path)という.道および有向道は,少なくとも1本の枝を含み, その始点と終点が一致するとき,閉路(closed path (cycle))および有向閉路(directed closed path (directed cycle))と呼ばれる.平面上に枝を交差させることなく幾何学的に表現することが可能なグラフを平面グラフ (planar graph) という.閉路を含まない連結なグラフを木 (tree)という.グラフ
への道(あるいは路)(path) という.その道上の枝がたどる向きにすべて揃っているとき,そのような道を有向道(あるいは有向路)(directed path)という.道および有向道は,少なくとも1本の枝を含み, その始点と終点が一致するとき,閉路(closed path (cycle))および有向閉路(directed closed path (directed cycle))と呼ばれる.平面上に枝を交差させることなく幾何学的に表現することが可能なグラフを平面グラフ (planar graph) という.閉路を含まない連結なグラフを木 (tree)という.グラフ の点集合
の点集合 のある2分割
のある2分割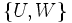 が存在して,各枝が
が存在して,各枝が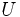 の点と
の点と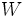 の点を結ぶとき,このグラフ
の点を結ぶとき,このグラフ を2部グラフ (bipartite graph) という.
を2部グラフ (bipartite graph) という.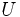 と
と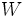 の点の数がそれぞれ
の点の数がそれぞれ と
と であって,
であって,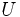 の各点と
の各点と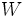 の各点を結ぶ枝が丁度1本存在するとき,この2部グラフを完全2部グラフと言い,
の各点を結ぶ枝が丁度1本存在するとき,この2部グラフを完全2部グラフと言い, 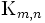 のように表す.グラフ
のように表す.グラフ が自己閉路(1本の枝からなる閉路)を含まず, そのすべての相異なる2点に対してそれらを結ぶ丁度1本の枝が存在するとき,このグラフを完全グラフ (complete graph)(あるいは完備グラフ)という.ここで,
が自己閉路(1本の枝からなる閉路)を含まず, そのすべての相異なる2点に対してそれらを結ぶ丁度1本の枝が存在するとき,このグラフを完全グラフ (complete graph)(あるいは完備グラフ)という.ここで, の点の数が
の点の数が であるとき,これを
であるとき,これを 点完全グラフと呼び,
点完全グラフと呼び, 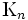 のように表す.
のように表す.
二つのグラフ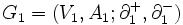 と
と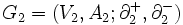 に対して, グラフ
に対して, グラフ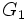 の点と枝の接続関係は保ったまま
の点と枝の接続関係は保ったまま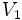 の各点の名前(ラベル)を変えて
の各点の名前(ラベル)を変えて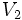 とし,同時に
とし,同時に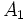 の各枝の名前(ラベル)を変えて
の各枝の名前(ラベル)を変えて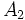 としてグラフ
としてグラフ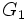 からグラフ
からグラフ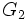 を得ることが可能であるとき, これらの二つのグラフは同形である (isomorphic)という.また,二つのグラフ
を得ることが可能であるとき, これらの二つのグラフは同形である (isomorphic)という.また,二つのグラフ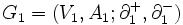 と
と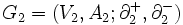 に対して,
に対して, 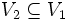 ,
, 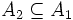 であり,
であり,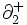 が
が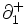 を,
を,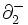 が
が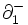 を,それぞれ,
を,それぞれ,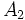 上に制限したものになっているとき, グラフ
上に制限したものになっているとき, グラフ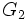 をグラフ
をグラフ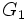 の部分グラフという.与えられたグラフ
の部分グラフという.与えられたグラフ の幾何学的表現から,いくつかの枝を消し,いくつかの孤立して残る点を消して得られる幾何学的表現に対応するグラフが元のグラフ
の幾何学的表現から,いくつかの枝を消し,いくつかの孤立して残る点を消して得られる幾何学的表現に対応するグラフが元のグラフ の部分グラフである.
の部分グラフである.
[1] C. Berge, Graphes et Hypergraphes, Dunod, 1970. 伊理正夫 他 訳,『グラフの理論, I~III』, サイエンス社,1976.
[2] J. A. Bondy and U. S. R. Murty, Graph Theory with Applications, North-Holland, 1976.
[3] R. Diestel, Graph Theory, 3rd ed., Springer, 2005. 根上生也,太田克弘 訳, 『グラフ理論』, シュプリンガー・フェアラーク東京,2000.
[4] F. Harary, Graph Theory, Addison-Wesley, 1969. 池田貞雄 訳,『グラフ理論』, 共立出版,1971.
| グラフ・ネットワーク: | TSP多面体 クラスカル法 クラスター分析 グラフ シュタイナー最小木 ダイクストラ法 ダルメジ・メンデルゾーン分解 |
graph
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2022/02/18 04:45 UTC 版)
※この「graph」の解説は、「グラフ」の解説の一部です。
「graph」を含む「グラフ」の記事については、「グラフ」の概要を参照ください。
「graph」の例文・使い方・用例・文例
- “Photo”は“Photograph”の略だ
- graphのページへのリンク


