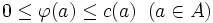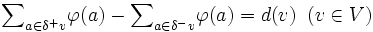ネットワークフロー問題
【英】:network flow problem
概要
ネットワーク上のフローを扱う最適化問題の総称. 最大フロー問題, 最小費用フロー問題, 輸送問題, 多品種フロー問題, 利得/損失付きフロー問題(一般化フロー問題)などがある. 最短路問題, 割当問題, 最小カット問題もネットワークフロー問題として扱うこともある.
詳説
ネットワーク上のモノの流れを扱う.モノは与えられた有向グラフ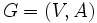 の各枝に沿って流れ,点で分岐や合流をする.ただし,各枝
の各枝に沿って流れ,点で分岐や合流をする.ただし,各枝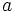 の容量
の容量 を超えず,各点
を超えず,各点 から出る正味の流量が,与えられた供給量
から出る正味の流量が,与えられた供給量 と等しくなるようにする.枝aを流れる量を
と等しくなるようにする.枝aを流れる量を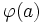 としたとき,
としたとき,
を満たす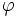 をフローといい,フローを扱った最適化問題をネットワークフロー問題という [1] .ただし,
をフローといい,フローを扱った最適化問題をネットワークフロー問題という [1] .ただし,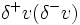 は点
は点 から出る (へ入る) 枝の全体を表す.
代表的なネットワークフロー問題に最大フロー問題がある.最大フロー問題とは,特別な点として入口
から出る (へ入る) 枝の全体を表す.
代表的なネットワークフロー問題に最大フロー問題がある.最大フロー問題とは,特別な点として入口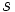 と出口
と出口 があり,
があり,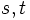 以外での供給量
以外での供給量 が0であるとき,
が0であるとき,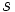 から入る量 (フロー値) を最大にするようなフロー (最大フロー) を求める問題であり,以下のように定式化できる.
から入る量 (フロー値) を最大にするようなフロー (最大フロー) を求める問題であり,以下のように定式化できる.
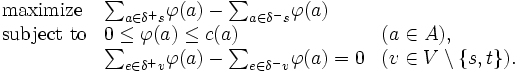
点の部分集合 が
が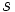 を含み,
を含み, を含まないとき,
を含まないとき, を
を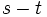 カットという.始点が
カットという.始点が にあり終点が
にあり終点が にない枝の容量の和を
にない枝の容量の和を の容量といい,容量最小の
の容量といい,容量最小の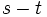 カットを最小カットという.任意のフローのフロー値は任意の
カットを最小カットという.任意のフローのフロー値は任意の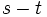 カットの容量よりも大きくなり得ない.この値が一致するようなフローと
カットの容量よりも大きくなり得ない.この値が一致するようなフローと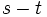 カットが存在することを示したのが,最大フロー最小カット定理 [2] である.実際,ある
カットが存在することを示したのが,最大フロー最小カット定理 [2] である.実際,ある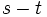 カットの容量に一致するフロー値をもつフローが以下の操作で得られる.
カットの容量に一致するフロー値をもつフローが以下の操作で得られる.
まず,任意のフロー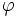 に対し,補助ネットワーク
に対し,補助ネットワーク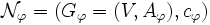 を定義する.
を定義する.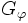 は,与えられたグラフと同じ点集合
は,与えられたグラフと同じ点集合 をもち,枝集合が
をもち,枝集合が のグラフとする.ただし,
のグラフとする.ただし,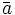 は,枝
は,枝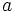 の向きを逆にした枝である.
の向きを逆にした枝である.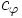 は,
は,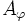 の枝に定義される残余容量であり,
の枝に定義される残余容量であり,
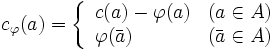
で与えられる.補助ネットワーク上の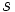 から
から への有向道を増加道という.増加道に沿ってフローの更新を繰り返し,フロー値を増加させる方法を増加道法という.任意のフローから始め,以下の手順を繰り返す.
への有向道を増加道という.増加道に沿ってフローの更新を繰り返し,フロー値を増加させる方法を増加道法という.任意のフローから始め,以下の手順を繰り返す.
手順1: 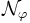 を作成し,増加道
を作成し,増加道 をみつける.増加道がなければ終了.
をみつける.増加道がなければ終了.
手順2: 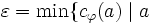 は
は 上の枝
上の枝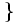 を求め,
を求め, 上のすべての枝
上のすべての枝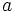 に関して,
に関して,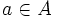 ならば,
ならば,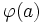 を
を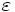 増加し,
増加し,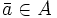 ならば,
ならば,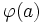 を
を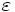 減少させる.
減少させる.
増加道が存在しなくなったとき,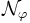 上で
上で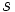 から到達可能な点集合を
から到達可能な点集合を とすると,
とすると, は
は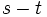 カットであり,その容量はフロー値と一致する.よって,増加道法が終了したときのフローが最大フローであり,
カットであり,その容量はフロー値と一致する.よって,増加道法が終了したときのフローが最大フローであり, が最小カットである.
が最小カットである.
増加道の選択を,枝数最小や,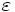 最大の基準で行うと,多項式時間の最大フローアルゴリズムとなる.一方,流量保存則を緩和したプリフローを用い,増加道が存在しないようなプリフローを維持しながら,最大フローを求めるプッシュ・再ラベル法も効率よい最大フローアルゴリズムである.
最大の基準で行うと,多項式時間の最大フローアルゴリズムとなる.一方,流量保存則を緩和したプリフローを用い,増加道が存在しないようなプリフローを維持しながら,最大フローを求めるプッシュ・再ラベル法も効率よい最大フローアルゴリズムである.
最小費用フロー問題もネットワーク・フロー問題の一つである.各枝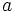 のフロー1単位あたりの費用
のフロー1単位あたりの費用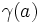 が与えられているとき,総費用
が与えられているとき,総費用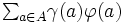 を最小にするフローを求める問題である.特に,すべての点で供給量
を最小にするフローを求める問題である.特に,すべての点で供給量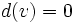 のとき,循環フローという.また,輸送問題も最小費用フロー問題の特殊ケースである.複数の供給地と需要地があり,各々の供給/需要量と,各供給地と需要地間の輸送費用がわかっているとき,供給/需要を満たし,輸送にかかる総費用を最小とする輸送方法とその輸送量を決定する輸送問題は,容量制約のない2部グラフ上の最小費用フロー問題である.
最小費用フローアルゴリズムも多数ある.補助ネットワーク
のとき,循環フローという.また,輸送問題も最小費用フロー問題の特殊ケースである.複数の供給地と需要地があり,各々の供給/需要量と,各供給地と需要地間の輸送費用がわかっているとき,供給/需要を満たし,輸送にかかる総費用を最小とする輸送方法とその輸送量を決定する輸送問題は,容量制約のない2部グラフ上の最小費用フロー問題である.
最小費用フローアルゴリズムも多数ある.補助ネットワーク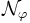 上の費用を
上の費用を
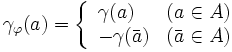
で定義すると,フローが最小費用である必要十分条件は,その補助ネットワーク上に負の費用の閉路が存在しないことである.補助ネットワーク上の負の費用の閉路を繰り返し除去することによって最適フローを求めるのが負閉路消去法である.この他にも,点に対応する双対変数を与え,相補スラック条件を満たす枝からなるネットワーク上で最大フロー問題を繰り返し解く方法,最短路問題を繰り返し解く方法,単体法を用いたネットワーク単体法などがある.いずれの方法も強多項式時間アルゴリズムが存在する.
最大フロー問題,最小費用フロー問題ともに,容量,供給量が整数で与えられているときには,整数値の最適フローが存在することが知られている.また,ネットワークの構造を用いた効率よいアルゴリズムがいくつか存在する.一方,1つのネットワーク上に複数品種を流す多品種フロー問題は,品種ごとに流量保存則が満たされており,かつすべての品種をあわせて容量制約が満たされている多品種フローを扱う.多くのアルゴリズムは線形計画法の手法に基づいている.整数値の多品種フローを求める問題はNP完全である.
[1] R. K. Ahuja, T. L. Magnanti and J. B. Orlin, Network Flows: Theory, Algorithms, and Applications, Prentice Hall, 1993.
[2] L. R. Ford, Jr. and D. R. Fulkerson, Flows in Networks, Princeton University Press, 1962.
[3] B. Korte and J. Vygen, Combinatorial Optimization, 4th ed., Springer, 2007. 浅野孝夫 他 訳, 『組合せ最適化』, シュプリンガー・フェアラーク東京,2005.
[4] アルゴリズムデータベース http://www-or.amp.i.kyoto-u.ac.jp/algo-eng/db/
| グラフ・ネットワーク: | デルタマトロイド ナップサック問題 ネットワーク ネットワークフロー問題 フェンシェル型双対定理 プリム法 ベルマン・フォード法 |
| 組合せ最適化: | グレブナー基底 データ構造 ナップサック問題 ネットワークフロー問題 ハッシュ表 パーフェクトグラフ パーフェクトグラフ予想 |
ネットワークフロー問題
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/06/07 07:50 UTC 版)
ネットワークフロー問題(ネットワークフローもんだい、英: network flow problems)とは、組合せ最適化の(グラフの辺上に容量の値が課せられた)フローネットワークにおいて各頂点において入るフローと出るフローが同じ量でかつすべての辺において流れるフローがその辺の容量以下となるようなフローを求める問題である[1]。
ネットワークフロー問題における特筆すべき問題としては以下のものが挙げられる:
- 最大流問題:フローネットワークにおいて始点となる頂点から終点となる頂点へ向けてフローを流すとき、最大のフローとなるものを求める問題である[1]:166-206。
- 最小費用流問題:辺に単位当たりのフローを流すのにかかる費用が与えられたフローネットワークにおいて始点から終点へ向けて決められた量のフローを流すときに、最小の費用で流すものを求める問題である[1]:294-356。
- 多品種流問題:フローネットワークにおいてそれぞれ相異なる複数のフローを同時に流すときに最小の費用となるものを求める問題である[1]:649-694。
最大流最小カット定理では最大流問題における最大流の値がフローネットワークの頂点のに分割を考え、そらを結ぶ辺の重みの和が最小となる頂点分割を求める最小カット問題の重みの和の値と一致することが知られている。また、近似最大流最小カット定理は、最大流最小カット定理を多品種流問題に拡張した定理である。無向フローネットワークでのゴモリー・フー木は任意の二つの頂点における最小カットを得ることができる。
フローを構築的に求めるアルゴリズムとしては以下のものが知られている:
- ディニッツ法:最大流問題に対する強多項式時間アルゴリズム[1]:221-223
- エドモンズ・カープ法:効率よく最大流問題の最適解を求める強多項式時間アルゴリズム
- フォード・ファルカーソン法:最大流問題に対する解法で貪欲法の一種である。一般的な問題に対しては強多項式時間アルゴリズムではない。
- ネットワーク単体法:線形計画問題に対する解法の単体法をネットワークフロー問題に特化させたアルゴリズム[1]:402-460
- アウトオブキルタ法:最小費用流問題に対する解法[1]:326-331
- プリフロープッシュ法:最大流問題に対して最も効率よく解くことができる解法の一種。
これらに挙げられる問題以外を解く方法としては線形計画問題として定式化を与えることが多くの場合で可能であり、それにより線形計画問題を解く最適化ソルバにより解くことが可能である。
脚注
関連項目
- ネットワークフロー問題のページへのリンク