最短路問題
【英】:shortest path problem
概要
有向グラフの各枝に長さが付与されたネットワークにおいて, 指定された2点間の有向道の中で最短の長さをもつもの(最短路)を見出す組合せ最適化問題. ナップサック問題, PERT等様々な問題が最短路問題とも関係し, さらに, ネットワークフロー問題や配送計画等のより複雑な問題の子問題として出現することも多い. ダイクストラ法やベルマン・フォード法等を用いて解くことができる. 無向グラフに対しても同様に定義される.
詳説
有向グラフ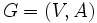 の各枝
の各枝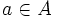 に長さ
に長さ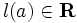 が付与されているネットワーク
が付与されているネットワーク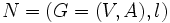 が与えられているとする. 有向グラフ
が与えられているとする. 有向グラフ の任意の2点
の任意の2点 に対して, 点
に対して, 点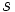 を始点とし点
を始点とし点 を終点とする有向道
を終点とする有向道 の長さ
の長さ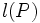 は
は 上の枝の長さの総和,
上の枝の長さの総和, 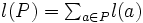 , と定める. 始点
, と定める. 始点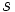 から終点
から終点 への有向道
への有向道 のなかで, その長さを最小にするもの(が存在すれば, それ)を点
のなかで, その長さを最小にするもの(が存在すれば, それ)を点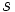 から点
から点 への最短路(shortest path)といい, 最短路を求める問題を最短路問題 (shortest path problem) という. 与えられたネットワークにおいて負の長さの有向閉路(負閉路と呼ぶ)が存在する場合には一般に最短路は存在しなくなる. ただし,負閉路を持つネットワーク上でも,初等的な(点を繰り返さない)道で最短なものを求める問題を考えることもあるが,一般的には解くことが難しい問題となる.
への最短路(shortest path)といい, 最短路を求める問題を最短路問題 (shortest path problem) という. 与えられたネットワークにおいて負の長さの有向閉路(負閉路と呼ぶ)が存在する場合には一般に最短路は存在しなくなる. ただし,負閉路を持つネットワーク上でも,初等的な(点を繰り返さない)道で最短なものを求める問題を考えることもあるが,一般的には解くことが難しい問題となる.
最短路問題は組合せ最適化問題の中での最も基本的かつ重要な問題の一つである. 例えば, ナップサック問題, PERT, 巡回セールスマン問題など様々な組合せ最適化問題が最短路問題とも関係し, 最短路問題において得られた知識はそれらの組合せ最適化問題の解法にも影響を与えている. また, 交通計画や通信ネットワークの分野などでは最短路問題を利用し解析に必要な基本データを算出している. さらに, ネットワークフロー問題, 配送計画問題やネットワークデザインなどのより複雑な問題に対するアルゴリズムにおいて,子問題として最短路問題を解くことがしばしば要求され, その応用は広範囲におよぶ ([2]).
最短路問題に対して様々なアルゴリズムが提案されている ([1, 6]). それらのアルゴリズムは, それが適用できるネットワークの種類から大きく二つに分類できる. 一つは, 負の長さの枝が存在しても適用できるアルゴリズムで, もう一つは, 負の長さの枝が存在しない時にのみ適用できるアルゴリズムである.
前者のタイプのアルゴリズムとしては, L. R. Ford [5] とR. E. Bellman [3] によって独立に示されたベルマン・フォード法(Bellman-Ford algorithm)(フォード・ベルマン法ともいう)が良く知られている. この方法では, 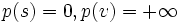
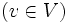 なる点のラベル
なる点のラベル を用意して, 枝
を用意して, 枝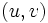 に対して
に対して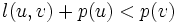 ならば
ならば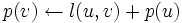 とおく.ここで,すべての枝に対して1回ずつこの操作を行うことを基本操作として,ラベルの減少が起る限り高々
とおく.ここで,すべての枝に対して1回ずつこの操作を行うことを基本操作として,ラベルの減少が起る限り高々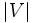 回基本操作を繰り返す.基本操作が
回基本操作を繰り返す.基本操作が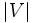 回繰り返された場合には負閉路が検出される.そうでない場合には, 終了時に得られたラベル
回繰り返された場合には負閉路が検出される.そうでない場合には, 終了時に得られたラベル によって,
によって,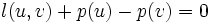 を満たす枝の全体からなる
を満たす枝の全体からなる の部分グラフ中の点
の部分グラフ中の点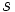 から各点
から各点 への有向道が最短路を与える.なお,ベルマン・フォード法の変種で隣接2点間の距離行列のべき乗と同等と見做される行列演算によって理解されるアルゴリズムとして,べき乗法(power method)も知られている. これらは
への有向道が最短路を与える.なお,ベルマン・フォード法の変種で隣接2点間の距離行列のべき乗と同等と見做される行列演算によって理解されるアルゴリズムとして,べき乗法(power method)も知られている. これらは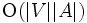 時間のアルゴリズムである.
時間のアルゴリズムである.
一方, すべての枝の長さが非負の時に,より高速に最短路を見出すタイプの代表的なアルゴリズムとして, E. W. Dijkstra [4] によって提案されたダイクストラ法 (Dijkstra's algorithm) が知られている.この方法では,出発点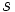 からの(最短)距離が小さい順に最短路および(最短)距離が確定していく.初期ラベル
からの(最短)距離が小さい順に最短路および(最短)距離が確定していく.初期ラベル はベルマン・フォード法と同じで, アルゴリズム実行中に最短路が確定した点集合を
はベルマン・フォード法と同じで, アルゴリズム実行中に最短路が確定した点集合を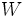 とすると,
とすると,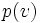
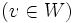 は点
は点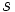 から点
から点 への(最短)距離に等しく,
への(最短)距離に等しく, 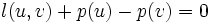 である枝
である枝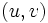 を通って
を通って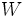 内において点
内において点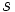 から点
から点 へ行く有向道が点
へ行く有向道が点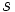 から点
から点 への最短路である.
への最短路である.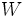 内で最後に(最短)距離が確定した点を
内で最後に(最短)距離が確定した点を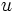 として,
として, 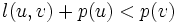 なる各点
なる各点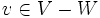 に対し
に対し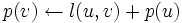 とおき,
とおき,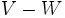 中でラベルの最小な点
中でラベルの最小な点 を見つけて
を見つけて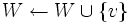 とおく.初期には
とおく.初期には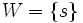 である.ダイクストラ法は
である.ダイクストラ法は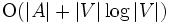 時間のアルゴリズムとして実現可能である.
時間のアルゴリズムとして実現可能である.
ベルマン・フォード法やダイクストラ法など現在提案されている最短路問題に対するアルゴリズムは本質的に始点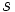 から全点までの最短路を同時に求める. 全点間の最短路を求めたい場合には, 1点から全点への最短路を求めるアルゴリズムを繰り返し適用し求めればよい.この場合, 負の長さの枝が存在する場合には1点からの最短路問題を1回解いてすべての枝の長さを非負に等価変換することが可能であり, 基本的にダイクストラ法を
から全点までの最短路を同時に求める. 全点間の最短路を求めたい場合には, 1点から全点への最短路を求めるアルゴリズムを繰り返し適用し求めればよい.この場合, 負の長さの枝が存在する場合には1点からの最短路問題を1回解いてすべての枝の長さを非負に等価変換することが可能であり, 基本的にダイクストラ法を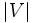 回適用する手間で解くことができる.なお,全点間最短路問題の
回適用する手間で解くことができる.なお,全点間最短路問題の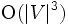 時間のアルゴリズムであるワーシャル・フロイド法 (Warshall-Floyd algorithm) も知られている.
時間のアルゴリズムであるワーシャル・フロイド法 (Warshall-Floyd algorithm) も知られている.
最短路問題は有向グラフ上で定義されているが, 無向グラフ上の最短路問題を考えたい場合には, 各枝をそれと同じ長さの互いに逆向きの有向枝で置き換えることにより, 有向グラフの場合に帰着することができる.ただし,負の長さの枝が存在する場合は, この帰着によって負閉路が含まれるので, 通常の最短路問題には帰着されない.
参考文献
[1] R. K. Ahuja, T. L. Magnanti and J. B. Orlin, Network Flows: Theory, Algorithms, and Applications, Prentice Hall, New Jersey, 1993.
[2] R. K. Ahuja, T. L. Magnanti and J. B. Orlin, "Applications of Network Optimization," in Network Models, M. O, Ball, T. L. Magnanti, C. L. Monma and G. L. Nemhauser, eds., North-Holland, 1995.
[3] R. E. Bellman, "On a routing problem," Quarterly of Applied Mathematics, 16 (1958), 87-90.
[4] E. W. Dijkstra, "A note on two problems in connexion with graphs," Numerische Mathematik, 1 (1959), 268-271.
[5] L. R. Ford, Jr., "Network Flow Theory," Report P-923, Rand Corp., Santa Monica,1956.
[6] 久保,田村,松井 (編) 『応用数理計画ハンドブック』,朝倉書店,2002.
[7] アルゴリズムデータベース http://www-or.amp.i.kyoto-u.ac.jp/algo-eng/db/
最短経路問題
(最短路問題 から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/08/02 08:30 UTC 版)
グラフ理論における最短経路問題(さいたんけいろもんだい、英: shortest path problem)とは、重み付きグラフの与えられた2つのノード間を結ぶ経路の中で、重みが最小の経路を求める最適化問題である。
種類
- 2頂点対最短経路問題
- 特定の2つのノード間の最短経路問題。一般的に単一始点最短経路問題のアルゴリズムを使用する。
- 単一始点最短経路問題 (SSSP:Single Source Shortest Path)
- 特定の1つのノードから他の全ノードとの間の最短経路問題。この問題を解くアルゴリズムとしては、ダイクストラ法やベルマン-フォード法がよく知られている。
- 全点対最短経路問題 (APSP : All Pair Shortest Path)
- グラフ内のあらゆる2ノードの組み合わせについての最短経路問題。この問題を解くアルゴリズムとしては、ワーシャル-フロイド法が知られている。
このような分類がされているのは、後者の問題が単に前者の問題を初期条件(ノード)を変えて繰り返し解くのではなく、アルゴリズムの過程で得た情報を利用して計算量を減らすことが可能となるからでもある。
単一始点最短経路問題
辺の重みなし有向グラフ
| アルゴリズム | 計算量 | 作者 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 幅優先探索 | 
|
||||||||||||||
| 非線形(制約付き) |
|
||||||||||||||
| 凸最適化 |
|
||||||||||||||
| 組合せ最適化 |
|
||||||||||||||
| メタヒューリスティクス | |||||||||||||||
- 最短路問題のページへのリンク

