楕円体法
【英】:ellipsoid method
概要
楕円体法(ellipsoid method) は, 微分不可能な凸計画問題に対する解法として, 1976年にユーディンとネミロフスキー(Yudin-Nemirovskii) によって提案された. その後1979年にカチヤン(L. G. Khachiyan)は, 楕円体法が線形計画問題に対する多項式時間解法 に成り得ることを示した. この結果は, 長年にわたって未解決のままであった,「線形計画問題を多項式時間で解くことが出来るか?」という計算複雑度に関する問題への肯定的な答を与えるものであり, 数理計画の分野に衝撃をもたらした. 線形計画法に対する解法としての楕円体法は, 実用の面からは単体法などに比べて効率が悪く, また理論的な計算量の面からも, 1984年以降に現れた内点法に劣っていることが分かっている. しかしながら, 線形, 非線形, 組合せなどの最適化問題に対し, 様々な理論的な結果を残している. 「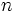 次元空間における楕円体を用いた2分探索」のような解法である.
次元空間における楕円体を用いた2分探索」のような解法である.
詳説
楕円体法を説明するために, 与えられた多面体 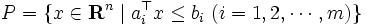 が空であるか否かを判定し, また空でなければ
が空であるか否かを判定し, また空でなければ  に含まれる点を求める, という非空性問題について考える. なお,
に含まれる点を求める, という非空性問題について考える. なお,  の上での線形関数
の上での線形関数 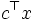 の最大化問題を解くには,
の最大化問題を解くには, 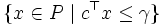 という多面体に対する非空性問題を繰り返し解き,
という多面体に対する非空性問題を繰り返し解き, 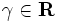 に関する2分探索を行えば良い.
に関する2分探索を行えば良い.
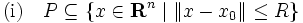 なる
なる 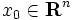 及び
及び 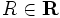 が既知である.
が既知である.
楕円体法では, いわば 「 次元空間での 楕円体を用いた2分探索」を行うことにより,
次元空間での 楕円体を用いた2分探索」を行うことにより,  の点を求める. 各反復では,
の点を求める. 各反復では,  を含む楕円体
を含む楕円体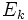 を常に保持する. 楕円体
を常に保持する. 楕円体 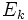 は, 中心と呼ばれるベクトル
は, 中心と呼ばれるベクトル  及び
及び 正定値対称行列
正定値対称行列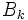 を用いて,
を用いて,
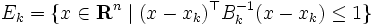 |
と表される. なお, 上記の仮定 (i) より, 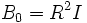 と選ぶことができる.
と選ぶことができる.
各反復では, 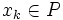 が成り立つか否かを調べる. 成り立つ場合はアルゴリズムを停止する. 成り立たない場合は,
が成り立つか否かを調べる. 成り立つ場合はアルゴリズムを停止する. 成り立たない場合は, 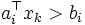 なる
なる  が存在するので, そのような
が存在するので, そのような  を見つける. 中心
を見つける. 中心 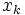 を通る超平面
を通る超平面 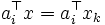 により,
により, 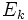 を半分にして得られる集合
を半分にして得られる集合 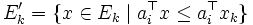 に対し, これを含み, かつ体積が最小の楕円体を
に対し, これを含み, かつ体積が最小の楕円体を  とおく. そのような楕円体
とおく. そのような楕円体  を表す
を表す 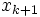 及び
及び 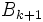 は 次のようにして求められる:
は 次のようにして求められる:
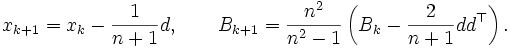 |
ここで, 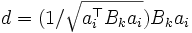 である.
である.
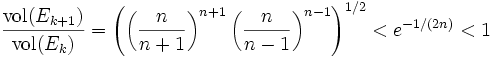 |
となる. したがって, 楕円体の体積は線形空間の次元  のみに依存する一定の比率で 減少していく. 反復回数
のみに依存する一定の比率で 減少していく. 反復回数  が十分大きくなり 楕円体の体積が
が十分大きくなり 楕円体の体積が 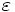 未満になった とすると, 仮定 (ii) により
未満になった とすると, 仮定 (ii) により  であることが分かるので, アルゴリズムを停止する.
であることが分かるので, アルゴリズムを停止する.  が多面体であることから, 仮定 (i), (ii) での
が多面体であることから, 仮定 (i), (ii) での 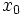 ,
,  ,
, 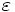 をうまく選ぶことができ, それにより多項式回の反復で終了することが導かれる.
をうまく選ぶことができ, それにより多項式回の反復で終了することが導かれる.
上記で述べた楕円体法の改良として,「深い」(deep)カットを用いた方法が 提案されている. この方法では, 半楕円体 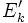 の代わりに, より小さな集合
の代わりに, より小さな集合 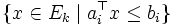 に注目し, それを含む最小の楕円体
に注目し, それを含む最小の楕円体  へと更新していく. この場合, 連続する2つの楕円体の比は,
へと更新していく. この場合, 連続する2つの楕円体の比は, 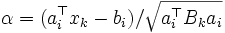 とおくと,
とおくと,
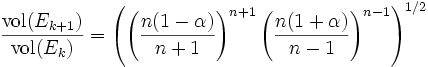 |
と表され, また  なので, 元の楕円体法に比べて反復回数が減少することがわかる.
なので, 元の楕円体法に比べて反復回数が減少することがわかる.
さらに, 代用(surrogate)カット, 平行(parallel)カットを用いれば, 楕円体の体積比をより減少させることができる. また, 深いカットと全く逆の考え方により得られる「浅い」(shallow)カットを用いると, 連続する楕円体の体積比は逆に増加するが, 理論的には, 他のカットでは得られない興味深い結果を得ることができる. これらのカットについての詳細は参考文献を参照されたい.
線形計画法に対する楕円体法の適用は, 線形計画のみならず組合せ最適化においても重要な結果を残している. その1つが, 最適化問題と分離問題の多項式時間に関する等価性であろう.
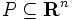 を多面体とする. ただし,
を多面体とする. ただし,  の不等式系による表現は必ずしも与えられていない, と仮定する. 分離問題とは, 任意のベクトル
の不等式系による表現は必ずしも与えられていない, と仮定する. 分離問題とは, 任意のベクトル 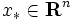 が与えられたとき,
が与えられたとき, 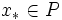 か否かを判定し,
か否かを判定し, 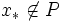 ならば
ならば 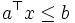
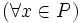 かつ
かつ 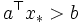 なる
なる 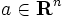 及び
及び 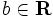 を求める問題のことである. 上記で述べた楕円体法のアルゴリズムを見ると分かるが, 必ずしも
を求める問題のことである. 上記で述べた楕円体法のアルゴリズムを見ると分かるが, 必ずしも  の不等式表現が陽に与えられている必要はなく, 各反復において
の不等式表現が陽に与えられている必要はなく, 各反復において  と
と 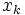 に関する分離問題を多項式時間で解けるならば, 最適化問題もまた多項式時間で解くことができる. 一方, この逆もまた成り立つことが Grötschel-Lovász-Schrijver (1981) 及び Padberg-Rao (1981) によって証明されている.
に関する分離問題を多項式時間で解けるならば, 最適化問題もまた多項式時間で解くことができる. 一方, この逆もまた成り立つことが Grötschel-Lovász-Schrijver (1981) 及び Padberg-Rao (1981) によって証明されている.
この他にも, 劣モジュラ関数の最小化やパーフェクトグラフでの最大 安定集合問題などの組合せ最適化問題が多項式時間で解ける, という結果が, 楕円体法の適用により導かれている.
[1] R. G. Bland, D. Goldfarb and M. J. Todd, "The ellipsoid method: a survey," Operations Research, 29(1981) 1039-1091.
[2] M. Grötschel, L. Lovász and A. Schrijver, Geometric Algorithms and Combinatorial Optimization, Springer-Verlag, 1991.
[4] G. L. Nemhauser, A. H. G. Rinnooy Kan and M. J. Todd, eds., Optimization, Handbooks in Operations Research and Management Science Vol. 1, North-Holland, 1989. 伊理正夫, 今野浩, 刀根薫 監訳,『最適化ハンドブック』,朝倉書店, 1995.
楕円体法
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/05/22 06:04 UTC 版)
楕円体法(だえんたいほう、英: ellipsoid method)とは数理最適化において凸集合内での凸関数最小化問題に対する反復法の一種である。楕円体法では各反復において楕円体を以前の反復より体積が小さくなるように生成し、凸関数の最小解集合を求める。
楕円体は有理数の入力データによる線形計画問題に対する多項式時間で解くアルゴリズムとなる。
歴史
楕円体法には長い歴史が存在する。楕円体法は反復法としてナウム・ショールによって始めて提案された。1972年には実数の凸最小化問題に対する近似アルゴリズムとしてアルカディ・ネミロフスキとデビッド・B・ユーディンによって研究されていた。
有理数入力データの線形計画問題に対する楕円体法としてはレオニード・カチヤンによって多項式時間で解くアルゴリズムとして提案・証明された。当時まで主に研究されていた単体法に関しては実用上では高速に動く解法であったが、理論的には指数時間アルゴリズムであったため、理論的に重要な成果であった。このことから、任意の入力に対して多項式時間を保証する楕円体の登場は大きな影響を与えた。
多項式時間を保証する線形計画問題に対するアルゴリズムがカチヤンの研究によって初めて示された。しかしながら実用上における楕円体法は計算速度が遅く、研究者の関心は低かった。にもかかわらず、後の線形計画問題に関する研究に大きな影響を与え、より実用的で多項式時間を保証する解法の提案につながった。特に初の多項式時間を保証する線形計画問題に対する内点法のカーマーカー法は実用上も楕円体法よりも高速で実行し、最悪時間計算量も楕円体法よりも勝る。
楕円体法は最悪時において制約の行数に依らず問題の次元・サイズにのみ依存する計算量を持つことから、組合せ最適化理論において重要な役割を長年果たしてきた[1][2][3][4]。21世紀になり楕円体法と同等の計算量を持つ内点法も登場するようになった[要出典]。
説明
凸最適化問題は以下の式から構成される。
- 凸関数

Optimization computes maxima and minima.
| 一般 | |
|---|---|
| 微分可能 |
| 凸最小化 | |||||||
|---|---|---|---|---|---|---|---|
| 線形 および 二次 |
|
| 系列範例 (Paradigms) |
|||||
|---|---|---|---|---|---|
| グラフ理論 |
|
||||
| ネットワークフロー (最大流問題) |
- 楕円体法のページへのリンク
 が空でな
が空でな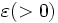 以
以