楕円
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2024/01/06 07:31 UTC 版)
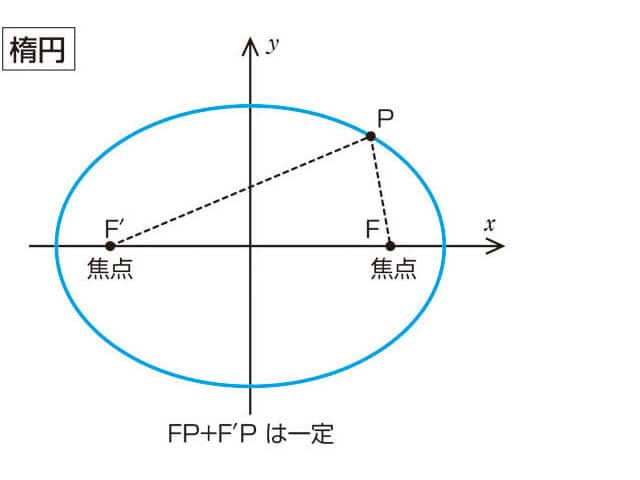
楕円（だえん、正字: 橢圓、英: ellipse）とは、平面上のある2定点からの距離の和が一定となるような点の集合から作られる曲線である。
- ^ Weisstein, Eric W. "Gauss-Kummer Series". mathworld.wolfram.com (英語).
- ^ Cetin Hakimoglu-Brown iamned.com math page
楕円（オーバル・ヘッド）
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2022/05/09 05:09 UTC 版)
わずかに楕円の頭を持ち、適合するドライバーでなければ廻すことができない。締め付けトルクはかなり大きく、防犯性にも富む。丸皿頭の変形である。
※この「楕円（オーバル・ヘッド）」の解説は、「ねじ」の解説の一部です。
「楕円（オーバル・ヘッド）」を含む「ねじ」の記事については、「ねじ」の概要を参照ください。
楕円
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2021/11/15 08:07 UTC 版)
楕円では、軌道長半径とは長軸方向の半径である。軌道長半径を含む直線は中心と2つの焦点、楕円周上で最も曲率の大きい2点を通過する。円の場合には、軌道長半径は半径と一致する。 軌道長半径の長さ a {\displaystyle a} は、軌道短半径 b {\displaystyle b} , 離心率 e {\displaystyle e} , 半通径 ℓ {\displaystyle \ell } と次のような関係がある。 b = a 1 − e 2 , ℓ = a ( 1 − e 2 ) , a ℓ = b 2 . {\displaystyle {\begin{aligned}b&=a{\sqrt {1-e^{2}}},\\\ell &=a(1-e^{2}),\\a\ell &=b^{2}.\end{aligned}}} 1つの焦点と ℓ {\displaystyle \ell } を固定し、もう1つの焦点を一方向にどこまでも引き伸ばすと放物線が得られる。 a {\displaystyle a} と b {\displaystyle b} は無限大になるが、 a {\displaystyle a} の方が b {\displaystyle b} よりも早く増加する。 軌道長半径は、1つの焦点から楕円周上への1点に至る、最小距離と最大距離の平均値となる。極座標系で1つの焦点を原点、もう1つの焦点をx軸の正方向に置くと、 r ( 1 − e cos θ ) = ℓ {\displaystyle r(1-e\cos \theta )=\ell } となり、 r = ℓ 1 + e {\displaystyle r={\dfrac {\ell }{1+e}}} と r = ℓ 1 − e {\displaystyle r={\dfrac {\ell }{1-e}}} の平均値は a = ℓ 1 − e 2 {\displaystyle a={\dfrac {\ell }{1-e^{2}}}} となる。
※この「楕円」の解説は、「軌道長半径」の解説の一部です。
「楕円」を含む「軌道長半径」の記事については、「軌道長半径」の概要を参照ください。
楕円
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2021/11/19 09:01 UTC 版)
楕円の軌道短半径は、楕円の中心（焦点の間を結ぶ線分の中心）から楕円の端まで伸びる。軌道短半径は、短軸の半分の長さである。短軸は、長軸と直交して楕円の端を結ぶ線分のうち最も長いものである。 軌道短半径bは、軌道離心率 e {\displaystyle e} 、半通径 l {\displaystyle l} を用いて、軌道長半径 a {\displaystyle a} と以下のような関係がある。 b = a 1 − e 2 {\displaystyle b=a{\sqrt {1-e^{2}}}\,\!} a l = b 2 {\displaystyle al=b^{2}\,\!} 楕円の軌道短半径は、焦点からの距離の最大値 r m a x {\displaystyle r_{max}} と最小値 r m i n {\displaystyle r_{min}} 、即ち焦点から長軸の末端までの距離の幾何平均である。 b = r m a x r m i n . {\displaystyle b={\sqrt {r_{max}r_{min}}}.} 放物線は、lを変えずに、1つの焦点を固定してもう1つを一方向に任意に遠くに動かすことで得られる。従ってaもbも無限大になるが、aの方がbよりも速く大きくなる。 軌道短半径の長さは、以下の式でも表される。 2 b = ( p + q ) 2 − f 2 {\displaystyle 2b={\sqrt {(p+q)^{2}-f^{2}}}} ここで、fは焦点の間の距離、pとqはそれぞれの焦点から楕円内の点までの距離である。
※この「楕円」の解説は、「軌道短半径」の解説の一部です。
「楕円」を含む「軌道短半径」の記事については、「軌道短半径」の概要を参照ください。
楕円
「楕円」の例文・使い方・用例・文例
- シリウスを回る軌道は楕円形である。
- 冥王星は楕円形の軌道をしている.
- (ラグビー用などの)楕円形のボール.
- 楕円軌道
- 遊星の軌道の形は楕円形だ
- 遊星は楕円形をえがく
- スピードスケート（通常楕円形のコースの周りで）の競争スケート
- ボール（丸または楕円）を用いる様々なゲームで、2つの相対するチームが互いのゴールにそのボールを蹴り込んだり、運び込んだり、押し込んだりする
- 楕円形のボールを使って行われるフットボールの一形態
- 黄色、オレンジまたは赤い色素を生産する球状であるか楕円通常好気性真正細菌
- 白く縁取りされた暗い楕円形の斑点を持つ一般的な北アメリカの緑または茶色のカエル
- マルスダレガイ科の標準属：厚い楕円形の食用貝に属す
- （雌豚のような形の）楕円形の分節した体の陸生等脚類
- 円盤のような丸くまたは楕円形の
- 楕円面の性質か形を持っている
- 長球は、主軸を楕円に回転させることによって発生する
- 円筒形または楕円形の本体の
- （葉の形について）楕円の形で
- 大西洋・太平洋・地中海産の楕円形の色鮮やかな大型深海魚
- 楕円の側扁の体の暖海浅瀬に生息するほとんど知られていない夜行性の魚
- >> 「楕円」を含む用語の索引
- 楕円のページへのリンク
