円錐曲線

デジタル大辞泉

えんすい‐きょくせん〔ヱンスイ‐〕【円^×錐曲線】

読み方：えんすいきょくせん

直円錐の円錐面を、頂点を通らない平面で切ったときの切り口の平面曲線。切る傾きによって、円・楕円・双曲線・放物線ができる。二次方程式が円錐曲線に対応するところから、二次曲線ともいう。

宇宙用語辞典

円錐曲線 conic section

円、楕円、放物線や双曲線などを表す総称。

ウィキペディア

円錐曲線

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2024/09/30 09:53 UTC 版)

円錐の切断

円錐曲線（えんすいきょくせん、英語: conic curve）とは、円錐面を任意の平面で切断したときの断面、円錐断面（英語: conic section）として得られる曲線群の総称である。

歴史

古代ギリシャのアポロニウスが円錐曲線論の体系を著書にまとめ、中世ヨーロッパではケプラーによって天体の軌道との関連が見出された。またアポロニウスによる総合幾何学的な円錐曲線論はオイラーによって解析幾何学を用いて現代的に書き換えられた。

概要

• 
  楕円
• 
  放物線
• 
  双曲線
• 
  断面
• 
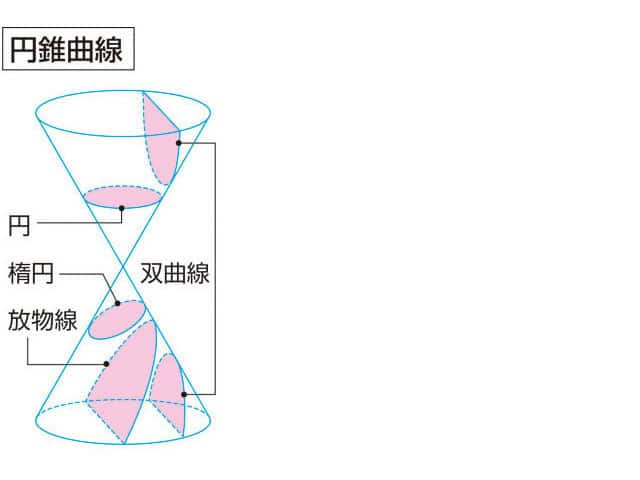
  円を含む円錐曲線の図の例（学問によっては、正円を円錐曲線に含まない。）

円錐曲線は、xy-平面 R² 上で定義され、次の陰関数曲線によって与えることが出来る。

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0\,$

• 円（全ての母線と交わり、底面に平行な平面で切断）

$X^{2}+Y^{2}=r^{2}\quad$

準線を共有する、いくつかの離心率 e に対応する円錐曲線

焦点を共有する、いくつかの離心率 e に対応する円錐曲線

別な定義のしかたとして、直線と、その直線上に含まれないような点 F を取り、点 F から直線への垂線に対して点 F のある方向が正と定めそれを x 軸とする。直線上で点 M' を動かすとき、その直角位置上で FM : MM' = e : 1 (e > 0) を満たすような点 M の集合は円錐曲線を描く。この時、FM と MM' の比の値 e を離心率といい、直線を準線、 点 F を焦点という。

ここで、焦点 F を極とする平面極座標 (r, θ) を新たにとれば、動点 P の軌道は

$r(\theta )={\frac {l}{1-e\cos \theta }}$

• フランス
• BnF data
• イスラエル
• アメリカ
• 日本
• チェコ

ウィキペディア小見出し辞書

円錐曲線

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2022/05/30 12:50 UTC 版)

「円 (数学)」の記事における「円錐曲線」の解説

詳細は「円錐曲線」、「楕円」、「放物線」、および「双曲線」を参照 2つの点（焦点と呼ばれる）からの距離の和が一定であるような点の軌跡を楕円という。楕円は一般に円を潰したような形をしており、楕円のうち特別な場合――2つの焦点が一点で一致する場合――が円である（このとき、焦点は「円の中心」と呼ばれる）。一般の楕円でなく円であることを特に明示したいときには、円のことを正円（せいえん）または真円（しんえん）と呼ぶことがある。

Wiktionary日本語版（日本語カテゴリ）

円錐曲線

出典:『Wiktionary』 (2021/09/13 12:40 UTC 版)

名詞

円錐 曲線（えんすいきょくせん）

1. (図形) 円錐を平面で切断して得られる断面の曲線。切断する場所によって、楕円（真円を含む）・放物線・双曲線のいずれかが得られる。

翻訳

• アイスランド語: keilusnið ^(is) 中性
• アルメニア語: կոնական հատույթ ^(hy)
• 英語: conic section ^(en)
• オランダ語: kegelsnede ^(nl) 女性
• カタルーニャ語: secció cònica ^(ca) 女性, cònica ^(ca) 女性
• ガリシア語: sección cónica ^(gl) 女性
• スウェーデン語: kägelsnitt ^(sv) 中性
• スペイン語: sección cónica ^(es) 女性, cónica ^(es) 女性
• セルビア・クロアチア語: čunjosječnica ^(sh) 女性, konika ^(sh) 女性
• タイ語: ภาคตัดกรวย ^(th) (pâak dtàt gruay)
• チェコ語: kuželosečka ^(cs) 女性
• デンマーク語: keglesnit ^(da) 中性
• ドイツ語: Kegelschnitt ^(de) 男性
• ノルウェー語:

  ニーノシュク: kjeglesnitt ⁽ⁿⁿ⁾ 中性

  ブークモール: kjeglesnitt ^(nb) 中性

• フィンランド語: kartioleikkaus ^(fi)
• フェロー語: keylusnið ^(fo) 中性
• ポーランド語: przekrój stożkowy 男性, stożkowa ^(pl) 女性
• ポルトガル語: cônica ^(pt) 女性, seção cônica ^(pt)
• ルーマニア語: conică ^(ro) 女性, secțiune conică ^(ro) 女性
• ロシア語: кони́ческое сече́ние ^(ru) 中性

Weblio日本語例文用例辞書

「円錐曲線」の例文・使い方・用例・文例

• 円錐曲線.
• 円錐曲線法
• 円錐曲線の凹面側の固定参照点
• 円錐曲線という,直円錐を切った時にできる切り口の曲線
• 円錐曲線上の共役点である2点
• 放物線という,円錐曲線