安定結婚問題

OR事典

安定結婚問題

読み方：あんていけっこんもんだい
【英】：stable marriage problem

同数の男性と女性が存在し, それぞれが異性に対して選好順序をもつと仮定する. 男女間の完全マッチングが与えられたとき, それが安定であるとは, マッチングに含まれない男性と女性の任意の対 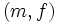に対して, が より現在の相手を好むか, または が より現在の相手を好むという性質が成り立つことである. 安定な完全マッチングを求める問題を安定結婚問題と呼ぶ. そのような解は常に存在し, ゲイル・シャプレーの解法により多項式時間で求められる.

「OR事典」の他の用語

グラフ･ネットワーク：

基本分割  多品種フロー  多項式時間アルゴリズム  安定結婚問題  完全グラフ  局所点連結度  局所辺連結度

ウィキペディア

安定結婚問題

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2025/08/02 09:06 UTC 版)

安定結婚問題（あんていけっこんもんだい、英: stable marriage problem）とはデイヴィッド・ゲールと ロイド・シャープレーによって1962年に提示された問題である。

安定結婚問題は n 人の男性と k 人の女性、および、各個人の選好順序からなる。選好順序とは各個人の好みに基づき異性全員と自分自身を全順序で並べたリストである。ここで、「自分自身」とは誰とも結婚せずに独身のままでいることを意味し、「参加者全員が独身であるよりも望ましい相手と結婚している」マッチングは個人合理性（英: individuality rationality）を満たすと定義される。安定結婚問題の解は安定なマッチングである。安定結婚問題に対し、互いに現在組んでいる相手よりも好きであるペア（以下ブロッキングペアとする）が存在せず、全員が個人合理性を満たすマッチングを安定マッチング（英: stable matching）という。

下図に安定結婚問題の例題とその例題の解となる安定なマッチング、および、安定でないマッチングを示す。 「：」以下が各個人の希望リストである。点線はブロッキングペアを表している。

全ての例題について、安定マッチングは必ず存在する。それを見つける O(N²) 時間アルゴリズムが存在することも知られている（下を参照）。

ゲール-シャープレー (Gale-Shapley) アルゴリズム

上で述べたように、安定結婚問題の例が与えられたとき安定マッチングは必ず 1 つ以上存在する。そのうちの 1 つ（ないし、2つ）を Gale と Shapley により提案された、ゲール-シャプレイ (Gale-Shapley) アルゴリズム（以下、G-S アルゴリズムと略す）を用いて求めることができる。その手順は、次の通りである。

入力：n 人の男性と k 人の女性、および、各人の異性全員に対する選好順序のリスト

出力：安定マッチング（つまり、男女 
     $\min\{n,k\}$ カテゴリ /  コモンズ