巡回セールスマン問題

デジタル大辞泉

じゅんかいセールスマン‐もんだい〔ジユンクワイ‐〕【巡回セールスマン問題】

読み方：じゅんかいせーるすまんもんだい

あるセールスマンが複数の都市を一度ずつ訪れるとき、どのような順番で巡回すれば総移動時間（移動距離または交通費）を最小にできるかを問う問題。グラフ理論の有名な問題の一つであり、都市（ノード）の数が大きくなると計算量が爆発的に増えることが知られている。同種の問題は、荷物の配送や集積回路の配線などに応用される。

IT用語辞典バイナリ

巡回セールスマン問題

読み方：ジュンカイセールスマンモンダイ
【英】traveling salesman problem

巡回セールスマン問題とは、組み合わせ最適化問題の一つで、「ある都市を出発したセールスマンの移動距離が最小値を取るように、すべての都市を一度ずつ必ず訪問して出発点に戻るための経路を求める」を求める問題のことである。旅商人問題とも言う。もともとは米ランド社が提出した懸賞問題である。

巡回セールスマン問題をコンピュータで特には、任意のnに対して最適解を求める解法のうち、最も短い時間で最適解が得られる解法でも、実行時間が2の二乗に比例する。それゆえ、現在の主流であるノイマン型デジタル計算機では、最適解を求めることが難しいといわれている。

このため、ニューラルネットワーク、進化論的（遺伝的アルゴリズム）アルゴリズムを利用した方法やアニーリング法といった生物を模倣した新しい計算手法の有効性を示す方法として、巡回セールスマン問題をいかに短時間で解けるかが試金石として利用されている。

なお、今日では運送会社の配送ルートの計画から、VLSIの設計など、その解法は様々な場面で応用されている。

情報処理のほかの用語一覧

アルゴリズム：

選択ソート  シェルソート  識別子  巡回セールスマン問題  昇順  シーケンシャルサーチ  挿入ソート

>>アルゴリズムカテゴリの他の用語

OR事典

巡回セールスマン問題

読み方：じゅんかいせーるすまんもんだい
【英】：traveling salesman problem (TSP)

概要

枝に重みを与えたグラフにおいて, すべての点を丁度1度ずつ訪問して元に戻る巡回路(ハミルトン閉路)のうち, 総重みを最小にするものを求める問題. グラフの枝が有向であるか無向であるかで大別する. 平面上(あるいは空間内)の点と各点の間の距離が与えられたとき, すべての点を訪問する順回路のうち最短のものを求める問題, と定義されることもある. 代表的な組合せ最適化問題の1つ.

詳説

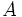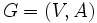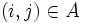　点集合 ，枝集合 から構成されるグラフ , 枝 上の距離 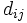が与えられたとき，点集合 のすべての点をちょうど1回ずつ経由する巡回路（ハミルトン閉路）で，枝の距離の合計を最小にするものを求める問題を巡回セールスマン問題 (traveling salesman problem) （行商人問題）とよぶ．

　特に，距離の対称性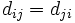（）を満たすものを対称巡回セールスマン問題，三角不等式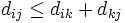（）を満たすものを三角不等式を満たす巡回セールスマン問題，点集合が 次元超立方体 内に分布しており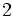， 点間の距離が点間のユークリッド距離で定義されたものをユークリッド巡回セールスマン問題 (Euclidean (Euclidian) traveling salesman problem) とよぶ．

　巡回セールスマン問題に対する応用は，数百点を扱う基盤配線，運搬経路計画，スケジューリング，数万点を扱う基盤穿孔，X線結晶構造解析 (タンパク質の構造解析)，数百万点を扱うVLSI設計など，さまざまである．また，次世代のVLSI設計においては，数千万点の問題を解く必要があると言われている．

　巡回セールスマン問題は，NP困難 (NP-hard) であり, 多項式時間の厳密解法が絶望視されているばかりでなく，近似比が 一定値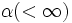 で抑えられる多項式時間の近似解法さえ 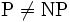のもとでは存在しないことが示されている．

　三角不等式を満たす対称巡回セールスマン問題に対しては，近似比が 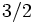以下の保証をもつ多項式時間の近似解法が知られている．また， を定数としたときの 次元ユークリッド巡回セールスマン問題に対しては，固定された 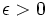を与えたときに，近似比が 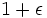以下に抑えられる多項式時間の近似解法（近似スキーム）が存在する．

　実用的な近似解法としては，最近近傍法 (nearest neighbor method) やセービング法 (saving method) によって構築された巡回路をk-opt法 (-opt)で改善する方法が一般的である．厳密解法としては，巡回セールスマン問題の多面体構造（TSP多面体(TSP polytope)）を利用した分枝カット法 (branch and cut method) が有効であり，実務的な大規模問題の求解に成功している．

---

参考文献

[1] 山本芳嗣, 久保幹雄,『巡回セールスマン問題への招待』, 朝倉書店，1997.

[2] D. L. Applegate, R. E. Bixby, V. Chvatal and W. J. Cook, The Traveling Salesman Problem, Princeton, 2006.

[3] アルゴリズムデータベース　http://www-or.amp.i.kyoto-u.ac.jp/algo-eng/db/

「OR事典」の他の用語

グラフ･ネットワーク：	完全グラフ  局所点連結度  局所辺連結度  巡回セールスマン問題  平面グラフ  循環フロー  最大フローアルゴリズム
組合せ最適化：	動的計画  多面体理論  多項式時間アルゴリズム  巡回セールスマン問題  整数計画  施設配置問題  最大クリーク問題

ウィキペディア

巡回セールスマン問題

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2025/03/06 07:48 UTC 版)

この記事は英語版の対応するページを翻訳することにより充実させることができます。（2024年9月） 翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。 英語版記事を日本語へ機械翻訳したバージョン（Google翻訳）。 万が一翻訳の手がかりとして機械翻訳を用いた場合、翻訳者は必ず翻訳元原文を参照して機械翻訳の誤りを訂正し、正確な翻訳にしなければなりません。これが成されていない場合、記事は削除の方針G-3に基づき、削除される可能性があります。 信頼性が低いまたは低品質な文章を翻訳しないでください。もし可能ならば、文章を他言語版記事に示された文献で正しいかどうかを確認してください。 履歴継承を行うため、要約欄に翻訳元となった記事のページ名・版について記述する必要があります。記述方法については、Wikipedia:翻訳のガイドライン#要約欄への記入を参照ください。 翻訳後、{{翻訳告知|en|Travelling salesman problem|…}}をノートに追加することもできます。 Wikipedia:翻訳のガイドラインに、より詳細な翻訳の手順・指針についての説明があります。

巡回セールスマン問題を総当たりで解く場合のイメージ。左側で一つずつ探していき、より効率のいいルートが見つかった場合、右側のグラフが更新される。

巡回セールスマン問題（じゅんかいセールスマンもんだい、英: traveling salesman problem、TSP）は、都市の集合と各2都市間の移動コスト（たとえば距離）が与えられたとき、全ての都市をちょうど一度ずつ巡り出発地に戻る巡回路のうちで総移動コストが最小のものを求める（セールスマンが所定の複数の都市を1回だけ巡回する場合の最短経路を求める）組合せ最適化問題である。

詳細

問題例の大きさは、都市の数で表される。この問題は、計算複雑性理論においてNP困難と呼ばれる問題のクラスに属する。すなわち、問題例の大きさに関する決定性の多項式時間アルゴリズムが見つかりそうにない、計算量的に困難な問題である。なお、この問題の特殊ケースとして考えられるハミルトン閉路問題は、NP困難であると共にNP完全と呼ばれるクラスにも属するので、扱いが異なる。

都市間の移動コストが三角不等式を満たす、すなわち移動コストを距離と呼べる部分問題（あるいは制約つき問題）も、NP困難である。都市を平面上の点、都市間の距離を平面上のユークリッド距離とする部分問題は最も直感的で理解しやすいが、これも NP困難である。この部分問題は平面TSPなどと呼ばれ、実用上の応用も多く、またベンチマークの問題例としても距離関数の定義が自明なため頻繁に現れる。 都市の間の移動コストを 1 または 2 に制限しても、この問題は NP困難である。ハミルトン閉路問題は、移動コストを 1 または無限大に制限した TSP とみなすことができる。

一方で制約のない巡回セールスマン問題の直接の応用事例は無いと言ってもよい。逆に実際の応用事例では、より複雑な定義で配送計画や表面実装ロボットの動作計画などに適用される。

整数線形計画問題による定式化

巡回セールスマン問題は整数線形計画問題として定式化することができる^[1][2][3]。定式化の方法としてはいくつか知られており、そのうち Miller–Tucker–Zemlin (MTZ) 定式化と Dantzig–Fulkerson（英語版）–Johnson（英語版） (DFJ) 定式化の2種類が著名な定式化として知られている。DFJ定式化はMTZ定式化と比べて制約式によって構成される多面体が厳密に小さいという意味で強い定式化とされているが、MTZ定式化についても特定の状況下では使用される^[4][5]。

両者の定式化に共通して与えられる定数は都市 ${\displaystyle 1,\ldots ,n}$

ウィキメディア・コモンズには、巡回セールスマン問題に関連するカテゴリがあります。