複雑ネットワーク
【英】:complex network
概要
現実世界で観察される, 何らかの特徴的な性質を持つグラフのこと. もしくは一般にそのような性質を持つグラフのこと. インターネット, WWWのハイパーリンク構造, 交友・知人関係,論文の引用関係,ニューラル・ネットワーク, たんぱく質の代謝反応など, グラフとして表現される現実の構造の多くは一見複雑な形状をしているが, 自明でない特徴的な性質を持つ. このようなグラフ構造を総称して複雑ネットワークという.
詳説
現実世界で観察される, 何らかの特徴的な性質を持つグラフのこと. もしくは一般にそのような性質を持つグラフのこと.
インターネット, WWWのハイパーリンク構造, 交友・知人関係, 論文の引用関係, ニューラル・ネットワーク, たんぱく質の代謝反応など, グラフとして表現される現実の構造の多くは一見複雑な形状をしているが, 自明でない特徴的な性質を共通して持つことが近年分かってきた. そこで, 現実の大規模なグラフ構造の持つ特徴を調べ, その特徴が現れる原理を解明する研究が急速に進展している.
なお, グラフにおいて点や辺に容量や長さなどの属性がある場合は特にネットワークと言うが, 複雑ネットワークの研究領域では, その区別は明確ではない. また, 特徴的な性質というものも明確に定まっているものではない.
複雑ネットワークの特徴的な構造として知られる代表的なものとして, まずスケールフリー (scale-free) がある. スケールフリーとは, 次数が である確率
である確率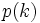 , つまり次数分布がべき乗則を満たすこと(
, つまり次数分布がべき乗則を満たすこと(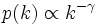 , ただし
, ただし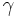 は正の実数)を意味する.
は正の実数)を意味する.
また, クラスタ係数に関しても特徴的な性質を持つことが多い. ここで, 次数 の点
の点 のクラスタ係数は, 隣接点間の辺数を
のクラスタ係数は, 隣接点間の辺数を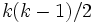 (つまり隣接点間辺数の取りうる最大値) で割ったものとして定義され, すべての点にわたるクラスタ係数の平均がそのグラフのクラスタ係数と定義される. 現実の複雑ネットワークのクラスタ係数は, 点数に関わらず比較的大きい値を取ることが知られている.
(つまり隣接点間辺数の取りうる最大値) で割ったものとして定義され, すべての点にわたるクラスタ係数の平均がそのグラフのクラスタ係数と定義される. 現実の複雑ネットワークのクラスタ係数は, 点数に関わらず比較的大きい値を取ることが知られている.
スモールワールド (small world) とは, 点数の多さに比較して平均点間距離が小さく, クラスタ係数が大きいことを指す. 単に平均点間距離が小さいことをスモールワールドということもある. この特徴を持つ現実の複雑ネットワークも多い.
現実の複雑ネットワークが, スケールフリーをはじめ上記で挙げたような性質を持つ原因を解明するために, 様々なモデルが検討されてきた.
複雑ネットワークの研究の興隆以前から知られていた, ErdösとRéyniのランダム・グラフは, 点集合の任意の二点間に確率的に辺を張ることでグラフを生成するモデルである. ただ, この次数分布はポアソン分布に従うため, スケールフリーではない. また, クラスタ係数は点数 の増加にしたがって
の増加にしたがって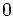 に収束する. ただし, 平均点間距離は
に収束する. ただし, 平均点間距離は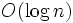 であって小さいと言える.
であって小さいと言える.
WattsとStrogatzは, 大きなクラスタ係数と小さい平均点間距離を同時に実現するスモールワールド・ネットワークのモデルを提案した. これは, 正方格子の辺集合の一部をランダムにつなぎかえるというものである. ただし, このモデルで生成されるグラフはスケールフリーではない.
BarabásiとAlbertによるBAモデルは, 時間の経過とともに点も付け加えられていく「成長」(growth) と, 新しく加わった点は次数の高い既存の点と高い確率で辺で繋がれる「優先的選択」(preferential attachment) という2つの原理を基本としており, スケールフリーであるグラフ(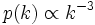 )を生成する. また, 点数
)を生成する. また, 点数 の時, 直径は
の時, 直径は であり, 平均点間距離は小さい. ただし, クラスタ係数は点数の増加にしたがって0に収束するため, 現実の複雑ネットワークとは違って小さい.
であり, 平均点間距離は小さい. ただし, クラスタ係数は点数の増加にしたがって0に収束するため, 現実の複雑ネットワークとは違って小さい.
「成長」と「優先的選択」に基づいたバリエーションとして, 次数の小さい点が選択的に非活性化して新しい点からの辺を受け取れなくなる頂点非活性化モデルなどがある. モデルにはランダム性が組み込まれていることが多いが, 決定的な規則によって点や辺を追加する階層的モデルというものもある.
「成長」と「優先的選択」とは異なる原理に基づくモデルとして閾値モデルというものがある. これは, 各点には重みが確率的に与えられており, 点 と
と の間には,
の間には,  と
と の重みの和や積 (一般的には二点の重みの関数) に基づいて確定的もしくは確率的に辺が張られるというものである. 点の重みが従う確率分布が指数分布に従う場合などに, スケールフリーであるグラフを生成することが分かっている. また平均点間距離は小さい. クラスタ係数は, 点数が増加しても有限な値に留まるため, 大きいと言える. 点間距離の効果も考慮した空間閾値モデルへの拡張もある.
の重みの和や積 (一般的には二点の重みの関数) に基づいて確定的もしくは確率的に辺が張られるというものである. 点の重みが従う確率分布が指数分布に従う場合などに, スケールフリーであるグラフを生成することが分かっている. また平均点間距離は小さい. クラスタ係数は, 点数が増加しても有限な値に留まるため, 大きいと言える. 点間距離の効果も考慮した空間閾値モデルへの拡張もある.
これらのように, 現実の複雑ネットワークの持つ性質を再現する様々なモデルが提案されているが, 利用する際には, 対象とする分野に応じて適切なモデルを選ぶことが必要である.
複雑ネットワークの性質の解明が進むにしたがって, それらの性質を持つグラフ上での相互作用やアルゴリズムに関する研究も進みつつある.
例えば, コンピュータウィルスの拡散過程の研究がある. 伝染病の拡散の研究は古くから行われており, SISモデルなどの確率過程のモデルがあったが, それらはグラフ構造を仮定していない. しかし, コンピュータウィルスの拡散はグラフ構造に強く依存するため, グラフ上のSISモデルであるコンタクト・プロセスをはじめ, 様々なモデルが研究されている. これらは基本的に, 各点が健康・病気・回復・ウィルス潜伏などの状態の一つを取り, 異なる状態の点が隣接すると, それぞれの点の状態が確率的に他の状態に遷移するというものである. BAモデルによって生成されたグラフでは, 感染のしやすさを表す感染確率が小さくても感染が広がりやすいことが知られている.
Webコミュニティ探索に関する研究も進展しつつある. これは, Webのハイパーリンク構造によるネットワーク (Webグラフ) 内にコミュニティを見出すことである. コミュニティの定義は様々であるが, 相互に密接にリンクを張っているページの集合, 言い換えればWebグラフ内の密な部分グラフという捉え方や, あるページ集合とそれらへリンクを張る (関心を同じくする) ページ集合のなす二部グラフという捉え方が一般的である. このようなコミュニティを発見することによって, 検索エンジンのカバー率の向上や, ディレクトリ検索型検索サイトのカテゴリの自動生成などに応用できる.
Kleinbergによって提案された, オーソリティとハブからなる二部グラフをコミュニティと考えるものは有名である. これは, 関連するページへ多くのリンクを持つページ (ハブ) は情報の連結点として重要であり, また多くのハブページからリンクされているページ (オーソリティ) は, そのトピックについて重要な情報を持つといういう考え方をベースとしている. Webグラフ構造から各ページのオーソリティとしての価値とハブとしての価値の高いものを選び出すことによってコミュニティを抽出する.
検索サイトのGoogleで採用されている, 検索結果の重要度を測るページランクという概念は, Webグラフ上のランダムウォークと密接に関係している. 点 のランクを
のランクを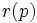 , 次数を
, 次数を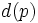 とした時,
とした時, 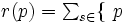 を終点とする有向辺の始点集合
を終点とする有向辺の始点集合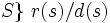 を満たすものとして, 各点のランクが定義される(ただし, すべての点のランクの和が1であるように正規化される). あるページのランクは, そこへリンクを張るページが多いほど, そしてリンク元のランクが高いほど高くなる. ただし, リンク元のページから外部へのリンクが多いと, それからの寄与は小さくなる. ページランクは, 有向グラフの遷移確率行列に基づくマルコフ過程にしたがうランダムウォークにおいて, 定常状態における各点での滞在確率に等しい.
を満たすものとして, 各点のランクが定義される(ただし, すべての点のランクの和が1であるように正規化される). あるページのランクは, そこへリンクを張るページが多いほど, そしてリンク元のランクが高いほど高くなる. ただし, リンク元のページから外部へのリンクが多いと, それからの寄与は小さくなる. ページランクは, 有向グラフの遷移確率行列に基づくマルコフ過程にしたがうランダムウォークにおいて, 定常状態における各点での滞在確率に等しい.
上記に挙げたものの他にも, うわさやデマの広がり, マーケティングにおける広告戦略, パケット制御・カスケード故障などの振る舞いや性能は, グラフ構造に強く依存しており, 現在も精力的に研究が進められている.
[1] 増田直紀, 今野紀雄, 『複雑ネットワークの科学』, 産業図書, 2005.
[2] A. -L. バラバシ,『新ネットワーク思考 -世界のしくみを読み解く』, NHK出版, 2002.
[3] D. J. Watts, Small Worlds, Princeton University Press, 1999.
[4] M. E. J. Newman, "The structure and function of complex networks," SIAM Review 45 (2003), 167-256.
[5] R. Albert, A. -L. Barabási, "Statistical mechanics of complex networks," Review of Modern Physics 74 (2002), 47-97.
複雑ネットワーク
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2024/12/17 00:19 UTC 版)



複雑ネットワーク(ふくざつネットワーク、complex networks)は、現実世界に存在する巨大で複雑なネットワークの性質について研究する学問である。
複雑ネットワークは、1998年に「ワッツ・ストロガッツモデル」という数学モデルが発表されたことを契機に、現実世界の様々な現象を説明する新たなパラダイムとして注目を集めている。多数の因子が相互に影響しあうことでシステム全体の性質が決まるという点において複雑系の一分野でもある。
概要
現実世界に存在するネットワークは多様であり、巨大で複雑な構造を有しているが、一定の共通する性質を見出すことができる。それらの性質は「スケールフリー性」(次数分布のべき乗則)、「スモールワールド性」、「クラスター性」と呼ばれている。「スケールフリー性」(次数分布のべき乗則)とは、例えば、一部の人は非常にたくさんの知人を持っているが、大多数の人々の知人の数は少ないという性質である。「スモールワールド性」とは、例えば、「世間は狭い」と言われるように、一見赤の他人に見えても、実際は中間に少数の人を介するだけでつながっているという性質である。「クラスター性」とは、例えば、「自分と知人Aさんがいるときに、自分もAさんもどちらも知っている共通の知人Bさんのような人が1人もいない」という状況はまずありえないという性質である。
従来、こうした社会的ネットワークの性質は主に社会学の研究対象となってきたが、1998年に発表された「ワッツ・ストロガッツモデル」という数学モデルが注目を集めた。ワッツ・ストロガッツモデルは、現実世界のネットワークに近いような性質を持つネットワークモデルを、極めて単純なアルゴリズムで生成するものである。この研究に触発される形で、現実世界のネットワークが持つ性質への関心が高まり、インターネット、食物連鎖、さらには論文の被引用関係や言語の文法構造といったネットワークにおいても共通の性質が発見された。
現実世界の様々な現象を説明する新たなパラダイムとして、複雑ネットワークの研究は現在急速に進展しており、他の研究分野との相互影響も活発化している[1]。今後、複雑ネットワークの科学は、ネットワークの問題が関連する多数の分野において、普遍性と重要性を増していくものと予想される。
背景

グラフ理論は、18世紀にレオンハルト・オイラーが創始した学問で、この場合のグラフは頂点と辺の集合である。グラフ G は頂点(ノード、サイトともいう)の集合 V = {v1, v2, ..., vn} と辺(枝、リンク、エッジ、ボンド、タイともいう)の集合 E = {e1, e2, ..., em} によって記述される[2]。頂点 i に繋がっている辺の本数をその頂点の次数 ki という[3]。右図の例では、頂点1の次数は2、頂点2の次数は3である。頂点と辺のパターンを変えることによって様々な特性を持つグラフが生成される。
1959年にポール・エルデシュとアルフレード・レーニは、グラフの一種であるランダムグラフを作るエルデシュ=レーニモデルを考案した。エルデシュ=レーニモデルは、各種の興味深い性質を有し、グラフの解析的な取り扱いを大きく進歩させた。だが、その後はグラフ理論の分野では目立った進展はあまり起きていなかった。
1960年代から70年代にかけて社会学で2つの動きがあった。第一は実験社会心理学者スタンレー・ミルグラムによる、いわゆるスモール・ワールド現象、日本語にすれば「世間は狭い」現象を実証しようという試みである[4]。ミルグラムは1967年に考案した実験において、アメリカ内陸部の住人に手紙を渡し、全く面識のない東海岸の受取人へ向けて、郵便ではなく知人(ファーストネームで呼び合うような親しい間柄)経由で転送するように依頼し、届くまでに何人の仲介者が必要かを調べた[4]。結果は、平均して6人を仲介するだけで届くというものであった[4]。この結果は現在では標語的に六次の隔たりと呼ばれる[4]。
第二は、社会学者マーク・グラノヴェッターが発見した「弱い紐帯の重要性」と呼ばれる性質である。グラノヴェッターは1973年の論文において、人々が職を探す活動をする際に有効な紹介者となるのは、親友や家族などの身近な付き合いのある「強い紐帯」の間柄ではなく、ごくまれに接するような「弱い紐帯」の間柄であることを見出した。
以降、こうした社会的ネットワークの性質は主に社会学の研究対象となってきたが、1998年にブレイクスルーが訪れた。コーネル大学の博士課程の学生だったダンカン・ワッツと指導教官だったスティーヴン・ストロガッツは、多数のホタルの明滅やコオロギの鳴き声が同調する現象を究明する中で、スモール・ワールド現象を説明する「ワッツ・ストロガッツモデル」(WSモデル)という数学モデルを考案し[5][6]、同様の性質が映画俳優の共演関係や、電力系統、線虫の神経細胞など、現実世界の様々なネットワークにも共通して存在することを発見した。研究成果は『ネイチャー』に発表され[7][6]、これに触発された研究によって、インターネット、食物連鎖、さらには論文の被引用関係や言語の文法構造といったネットワークにおいても同様の性質が発見された。こうして、社会学、経済学、情報工学、生物学などの幅広い分野において「複雑ネットワーク」という新たなパラダイムが注目を集めることになった。
現実世界のネットワークの性質




現実世界に存在するネットワークは多様であり、巨大で複雑な構造を有しているが、一定の共通する性質を見出すことができる。それらの性質は「スケールフリー性」(次数分布のべき乗則)、「スモールワールド性」、「クラスター性」と呼ばれている。
スケールフリー性
現実世界のネットワークが持つ第1の性質は「スケールフリー性」(次数分布のべき乗則)である。これは、一部の頂点が他のたくさんの頂点と辺で繋がっており、大きな次数を持っている一方で、その他の大部分はわずかな頂点としか繋がっておらず、次数は小さいという性質である。次数の大きな頂点は「ハブ」とも呼ばれる。
スケールフリー性は、社会学をはじめとするこれまでの研究により、現実世界のネットワークで幅広く観察されている。例えば、人々の持っている知人関係の数をみると、一部の人は非常にたくさんの知人を持っているが、大多数の人々の知人の数は限られている。WWWではごく少数の有名サイトが数百万単位のリンクを集めているが、大多数のサイトはわずかなリンク先からしかリンクされていない。生体内の相互作用でも、ごく一部のたんぱく質が多数のたんぱく質と反応する構造になっている。男女の性的関係でも、ごく一部の人は何百人という相手と関係するが、大多数の人々は限られた相手としか関係を持たない[8][9]。
数学的には、スケールフリー性は頂点が次数 k を持つ確率 p(k) の確率分布の裾が 




このように、グラフ理論における既存の数学モデルは現実社会のネットワークを表現する上では一長一短といったところであったが、1998年にブレイクスルーが訪れた。ダンカン・ワッツとスティーヴン・ストロガッツが「ワッツ・ストロガッツモデル」(WSモデル)を発表したのである。
ワッツ・ストロガッツモデルでは次のアルゴリズムでグラフを生成する。
- 全ての頂点を、近隣の a 個の頂点と格子(1次元格子)状に辺で繋ぐ。
- それらの辺を確率 p でランダムに張り替える。
パラメータ p を0とおけば格子、1とおけばランダムグラフとなる。p を0.1前後とすると、格子とランダムグラフをあわせもったような性質のグラフが生成される。ワッツ・ストロガッツモデルでは、ショートカットが形成される効果によって平均最短距離はほぼ L ∝ log n となり、スモールワールド性を満たす。同時に格子の構造を残していることで、クラスター係数は格子に近い値となりクラスター性をも満たす。
もっともワッツ・ストロガッツモデルにも限界があり、次数分布は格子とポアソン分布の中間となるのでスケールフリー性は満たさない。しかし、現実世界のネットワークに近いような性質を持つグラフを極めて単純なアルゴリズムで生成できることが関心を呼んだ。この研究に触発される形で、現実世界のネットワークが持つ性質への関心が高まり、またこの研究をさらに発展させた研究が続々と発表されていった。
バラバーシ・アルベルト・モデル(バラバシ・アルバートモデル)
1999年、バラバーシ・アルベルト・ラースロー(アルバート=ラズロ・バラバシ)[注釈 3]とアルベルト・レーカ[注釈 4]はスケールフリー性を持つグラフの数学モデルを考案し、「バラバーシ・アルベルトモデル」(バラバシ・アルバートモデル;BAモデル)と呼ばれる[11]。BAモデルでは次のようなアルゴリズムでグラフを生成する[11]。やはり、極めて単純なアルゴリズムである。
- m 個の頂点からなる完全グラフ Kmをスタートとする。
- 新しい頂点を1個追加する。その頂点から、すでに存在している m 個の頂点に対して辺を張る。このとき、辺が張られる確率は、それぞれの頂点のその時点での次数 k に比例するものとする。
- 2を、頂点が所定の数になるまで繰り返す。
BAモデルでは、既存の次数の大きな頂点に対して新しい辺が高い確率で加わってゆき、その頂点がハブへと成長してゆく(右の図では一番上にある頂点がハブに相当する)。このモデルでは頂点の次数分布は p(k) = 2m(m+1) / [k(k+1)(k+2)] ∝ k-3 となり γ = -3 のスケールフリー性を満たす。モデルはランダムグラフと似たところもあるので、平均最短距離は L ∝ log n となりスモールワールド性をも満たす。
BAモデルの弱点は、クラスター係数が0に近い小さな値となり、クラスター性を満たさないことである。だがその後、これらの研究をさらに発展させる形で、単純なアルゴリズムでありながら「スケールフリー性」「スモールワールド性」「クラスター性」という現実世界のネットワークの3つの特徴全てを満たすようなモデルが発表されている[12]。
スケールフリーグラフの頑強性と脆弱性
スケールフリーグラフが持つ注目すべき特性として、ネットワーク障害など「ランダムな故障や攻撃」に対して頑強性が高いことがあげられる。スケールフリーなトポロジーを持つネットワークでは、全頂点のうちのランダムに5パーセントがダウンしたとしても、代替経路の存在によって頂点間の接続を維持でき、系全体の平均経路長(平均最短距離)はほとんど変化しないのである。同じ頂点数、同じ辺数でトポロジーが異なる他のネットワークではこのような特性は見られない。頑強性は次数分布のベキ指数と関係がありベキ指数が 2 < γ < 3 の場合は非常に頑健性が高くなることがモデルにより示されている。[13]しかしながら、頑健性は両刃の剣である。見方を変えれば頑健性が高いということは感染症やコンピュータウイルスがネットワーク全体に広がり易いということでもあるからだ。実際、ランダムネットワークにおいては存在するウイルスあるいは流行の拡散に関する閾値(threshold)がスケールフリーネットワークでは存在しないため拡散しやすく退治するのも困難で時間がより長くかかることが判明している。
一方で、スケールフリーなネットワークは、特定の重要なハブをピンポイントで狙った攻撃に対しては脆弱であるという弱点も併せ持っている。次数の集中した上位5パーセントの頂点がダウンしたとすると、系全体の平均経路長は約2倍にまで増大してしまう[14]。
同様の特性は自然界の食物連鎖のネットワークでも観察されている。食物連鎖のネットワークは生物種のランダムな絶滅に対しては頑強であるが、特定の重要な種が絶滅すると大きな影響を受けてしまう。こうした点を考慮することは生物多様性に関する議論においても重要であろう[15]。
複雑ネットワーク研究の現状と今後
2008年現在、複雑ネットワークの研究は急速に進展しており、他の研究分野との相互影響も活発化している。そうした中で、「コミュニティ構造」などの現実世界のネットワークを分析するための新たな視点が提案され[16]、「スケールフリー性」「スモールワールド性」「クラスター性」といった従来からの分析指標はもはや“古典的”な部類に属するものとなりつつある[17]。
今後、複雑ネットワークの科学は、堅牢な通信ネットワークの構築、感染症の予防、口コミのマーケティングといった、ネットワークの問題が関連する多数の分野において、普遍性と重要性を増していくものと予想される。
分析用ツール
複雑ネットワークの解析では、可視化・統計解析などを行う際に計算機の力を借りることが不可欠である。現在では、様々な分析用ツールがフリーウェアとして利用できる。
- Pajek - Windows用ネットワーク解析ソフト。
- igraph - グラフ関連のアルゴリズムが実装されたパッケージ。Rでの実装もある。
- Cytoscape - マルチプラットフォーム対応のネットワーク可視化/解析ソフト。LGPLで配布されている。(日本語サイト)
脚注
注釈
- ^ Amaral, L.A.N. et al (2000) によれば、現実世界の全てのネットワークが完全なべき乗則の次数分布となるわけではない。辺が集中することで混雑などのコストが発生する場合は集中は頭打ちとなる。典型例は航空路線のネットワークである。
- ^ 「スモールワールド性」という用語の定義に関しては曖昧さがある。単にグラフの平均最短距離が小さい状態を指す場合もあれば、小さな平均最短距離と大きなクラスター係数とを共に満たす状態を指す場合もある。ランダムグラフは、前者の定義に従えばスモールワールドであり、後者に従えばスモールワールドではない。
- ^ Barabási Albert László [ˈbɒrabɑ̈ːʃi ˌɒrbɛrtˌlɑ̈ːsloː]。バラバーシが姓、アルベルトとラースローが名(男性名)。セーケイ人(ハンガリー人の一派)。ルーマニア領トランシルヴァニアのセーケイ地方のハルギタ県カルツファルヴァ村またはカルツ村(ルーマニア語名 クルツァ村)生まれ。国籍はルーマニアとハンガリーと米国の三重国籍。
- ^ Albert Réka [ˈɒrbɛrt ˌre̝ːkɒ]。アルベルトが姓、レーカが名(女性名)。セーケイ人(ハンガリー人の一派)。ルーマニア領トランシルヴァニアのセーケイ地方のマロシュ県サースレーゲン市(ルーマニア語名 レギン市)生まれ。国籍はルーマニアとハンガリーと米国の三重国籍。
出典
- ^ 右田・今野 2011, p. 14.
- ^ 右田・今野 2011, p. 26.
- ^ 今野・町田 2008, p. 46.
- ^ a b c d 今野・町田 2008, pp. 12–13.
- ^ 右田・今野 2011, p. 142.
- ^ a b 右田・今野 2011, p. 146.
- ^ Watts, D.J., and Strogatz, S.H. (1998)
- ^ F Liljeros et al. "The web of human sexual contacts". Nature, 411, pp.907-908(2001) オンライン・ペーパー
- ^ A. Schneeberger et al. "Scale-Free Networks and Sexually Transmitted Diseases" Sexually Transmitted Diseases, 31(6), pp.380-387(2004) オンライン・ペーパー
- ^ Albert, R., and Barabási, A.-L. (2002)
- ^ a b 右田・今野 2011, p. 162.
- ^ 例えば Dorogovtsev, S.N. et al. (2002) や Klemm, K., and Eguíluz, V.M. (2002)
- ^ Reuven Cohen , Shlomo Havlin (Jul 2010), RobustComplex Networks: Structure,ness and Function, Cambridge University Press, pp. 120, ISBN 978-0-521-84156-6
- ^ Albert, R. et al. (2000)
- ^ Solë, R.V., and Montoya, J.M. (2001)
- ^ Newman, M.E.J., and Girvan, M. (2004)
- ^ Costa, L.F. et al. (2005)
参考文献
論文
- Albert, R. et al., "Error and attack tolerance of complex networks", Nature 406, pp. 378-382 (2000)
- Amaral, L.A.N. et al, "Classes of small-world networks", Proceedings of the National Academy of Sciences of the United States of America 97, No. 21, pp. 11149-11152 (2000)
- Barabási, A.-L., and Albert, R., "Emergence of scaling in random networks", Science 286, pp. 509-512 (1999)
- Dorogovtsev, S.N. et al., "Pseudofractal Scale-free Web", Physical Review E 65, 066122 (2002)
- Klemm, K., and Eguíluz, V.M., "Growing scale-free networks with small-world behavior", Physical Review E 65, 057102 (2002)
- Newman, M.E.J., and Girvan, M., "Finding and evaluating community structure in networks", Physical Review E 69, 026113 (2004)
- Solë, R.V., and Montoya, J.M., "Complexity and fragility in ecological networks", Proceedings of the Royal Society B: Biological Sciences 268, No. 1480, pp. 2039 - 2045 (2001)
- Watts, D.J., and Strogatz, S.H., "Collective dynamics of small-world networks", Nature 393, pp. 440-442 (1998)
- R. Nishida, M.Mori, and T. Iba, "Analyzing Co-Purchase Network of CDs in Japanease Online Store",Internal Workshop and Conference on Network Science 2008
レビュー論文
- Albert, R., and Barabási, A.-L., "Statistical mechanics of complex networks", Reviews of Modern Physics 74, pp. 47-97 (2002)
- Costa, L.F. et al., "Characterization of complex networks: A survey of measurements", arXiv.org
- Dorogovtsev, S.N., and Mendes, J.F.F., "Evolution of networks", Advances in Physics 51, No.4, pp. 1079-1187 (2002)
- Newman, M.E.J., "The structure and function of complex networks", SIAM Review 45, pp. 167-256 (2003)
学術書
- Ben-Naim, E., Frauenfelder, H., and Toroczkai, Z., Complex Networks, Springer-Verlag (2004), ISBN 3-540-22354-1
- Dorogovtsev, S.N., and Mendes, J.F.F., Evolution of Networks: from biological networks to the Internet and WWW, Oxford University Press (2003), ISBN 0-19-851590-1
- Pastor-Satorras, R., and Diaz-Guilera, A., Statistical Mechanics of Complex Networks, Springer (2003), ISBN 3-540-40372-8
- 増田直紀、今野紀雄、『複雑ネットワークの科学』、産業図書、2005年2月、ISBN 4-7828-5151-0
- 今野紀雄・町田拓也、2008、『よくわかる複雑ネットワーク』第1版、秀和システム〈図解入門〉 ISBN 978-4-7980-2138-6
一般向け書籍
- Barabási, A.-L., Linked:The New Science of Networks, Perseus Books Group (2002), ISBN 0-7382-0667-9
- アルバート=ラズロ・バラバシ、青木薫(訳)、『新ネットワーク思考―世界のしくみを読み解く』、NHK出版、2002年12月、ISBN 4-14-080743-1
- Buchanan, M., Nexus: Small Worlds and the Groundbreaking Science of Networks, W W Norton & Co Inc (2002), ISBN 0-393-04153-0
- マーク・ブキャナン、阪本芳久(訳)、『複雑な世界、単純な法則―ネットワーク科学の最前線』、草思社、2005年2月、ISBN 4-7942-1385-9
- Strogatz, S.H., SYNC: The Emerging Science of Spontaneous Order, Hyperion Books (2003), ISBN 0-7868-6844-9
- スティーヴン・ストロガッツ、蔵本由紀(訳)、長尾力(訳)、『SYNC』、早川書房、2005年3月、ISBN 4-15-208626-2
- Watts, D.J., Small Worlds: The Dynamics of Networks Between Order and Randomness, Princeton Univ Pr (1999), ISBN 0-691-00541-9
- ダンカン・ワッツ、栗原聡(訳)、福田健介(訳)、佐藤進也(訳)、『スモールワールド―ネットワークの構造とダイナミクス』、東京電機大学出版局、2006年1月、ISBN 4-501-54070-2
- Watts, D.J., Six Degrees: The Science of a Connected Age, W W Norton & Co Inc (2003), ISBN 0-393-04142-5
- ダンカン・ワッツ、辻竜平(訳)、友知政樹(訳)、『スモールワールド・ネットワーク―世界を知るための新科学的思考法』、阪急コミュニケーションズ、2004年10月、ISBN 4-484-04116-2
- 増田直紀、今野紀雄、『「複雑ネットワーク」とは何か―複雑な関係を読み解く新しいアプローチ』、講談社ブルーバックス、2006年2月、ISBN 4-06-257511-6
- 右田正夫・今野紀雄、2011、『マンガでわかる複雑ネットワーク―巨大ネットワークがもつ法則を科学する』初版、ソフトバンククリエイティブ〈サイエンス・アイ新書〉 ISBN 978-4-7973-5641-0
関連項目
- 複雑ネットワークのページへのリンク
