指数分布
指数分布
指数分布
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2022/01/06 05:11 UTC 版)
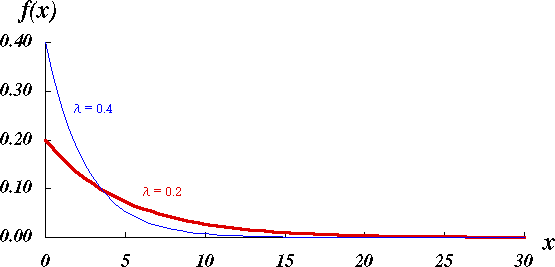
期待値を μ > 0 とする指数分布の累積分布関数 F ( x ) = 1 − e − x / μ {\displaystyle F(x)=1-e^{-x/\mu }} に対し、逆関数は F − 1 ( y ) = − μ ln ( 1 − y ) {\displaystyle F^{-1}(y)=-\mu \ln {(1-y)}} であり、 X = − μ ln ( 1 − U ) {\displaystyle X=-\mu \ln {(1-U)}} となる。1 − U も標準一様分布に従うため、高速化のために1 − U を U で置き換えた X = − μ ln ( U ) {\displaystyle X=-\mu \ln {(U)}} を使うことができる。この場合、U=0での処理に注意する必要がある。
※この「指数分布」の解説は、「逆関数法」の解説の一部です。
「指数分布」を含む「逆関数法」の記事については、「逆関数法」の概要を参照ください。
指数分布と同じ種類の言葉
- 指数分布のページへのリンク

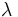 を
を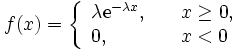
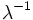 ,
, 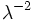 となる.
となる.



