平均値
平均値
変量 x の n 個の値を x1, x2, x3, …, xn とするとき、![[数式]](http://weblio.hs.llnwd.net/e7/img/dict/tmcyg/img/glossary_scheme_029.gif){kind=small}
を x の平均値という。
平均値（算術平均値）
分布の“重心”である。
有効ケース数を n，各ケースの測定値を Xi （ i = 1，2，… ，n ）とすると，以下の式で定義される。
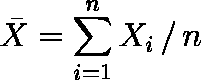
例題：5 つの測定値，2，3，4，7，9 の算術平均値を求めよ。
解答：
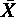= ( 2 + 3 + 4 + 7 + 9 ) / 5 = 5平均値が重心であることは，以下の図を見ればわかる。
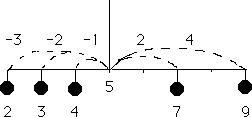
長い竿の 2，3，4，7，9 の位置に同じ重さの分銅が下がっている。これを 5 の位置（重心）でつるすと竿は水平になる。重心の左にある分銅が生み出すモーメントは -3-2-1 = -6，右にある分銅が生み出すモーメントは 2 + 4 = 6 となり，左右のモーメントが打ち消し合うので釣り合いがとれるのである。すなわち，
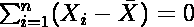である。度数分布表から平均値を求めるには，各階級の度数を fi ，その中心点を Xi ，m を階級数として，次式のように定義できる。
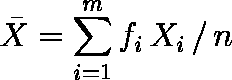
例題：「426 人の女子学生の身長の度数分布が表 1 のようであった。測定精度は無限小であるとして，平均値を求めよ。」
| 階級（単位 cm） | 度数 |
|---|---|
| 140 以上 145 未満 | 4 |
| 145 以上 150 未満 | 19 |
| 150 以上 155 未満 | 86 |
| 155 以上 160 未満 | 177 |
| 160 以上 165 未満 | 105 |
| 165 以上 170 未満 | 33 |
| 170 以上 175 未満 | 2 |
| 合計 | 426 |
解答：「測定精度が無限小」ということは，「140 以上 145 未満」の階級の中心点を 142.5 としてよいということである。
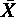= ( 4・142.5 + 19・147.5 + 86・152.5 + 177・157.5 + 105・162.5 + 33・167.5 + 2・172.5) / 426 = 67300 / 426 = 157.98平均値
平均
(平均値 から転送)
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2023/12/26 15:13 UTC 版)
平均（へいきん、英: mean, average, 独: Mittelwert, 仏: moyenne）または平均値（へいきんち、英: mean value, average value）とは、数学・統計学において、数の集合やデータの中間的な値を指す。欧米語の原意の中間（値）などと和訳することは少ない。
- ^ 最小二乗法において、加重和の最小化と加重平均の最小化は同じことである。
- ^ JIS Z 8101-1 : 1999, 2.13 平均.
- ^ 例えば A, B, C という3人の体重がそれぞれ 55 kg, 60 kg, 80 kg であったとすると、3人の体重の平均値は (55 kg + 60 kg + 80 kg) ÷ 3 = 65 kg である。
- ^ 民間給与実態統計調査結果 - 標本調査結果｜国税庁
- ^ Clementi, Fabio; Gallegati, Mauro (2005) "Pareto's law of income distribution: Evidence for Germany, the United Kingdom, and the United States", EconWPA
- ^ 西岡, 刈込平均 p.7.
- ^ 西岡, p.5.
- ^ 伏見, 第II章 確率論 10節 偶然量、平均値 p.70.
平均値
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2021/11/05 06:12 UTC 版)
瞬時値の正の範囲を1⁄2周期にわたって積分し、周期で割ったものを平均値（mean value）という。1⁄2周期をとるため半波平均値ともいうが、通常の正弦波交流の場合には1周期の瞬時値の算術平均がゼロであるため、単に「平均値」という場合には半波平均値を指す。 正弦波交流の平均値は次式のようになる。 E a v = 2 π E m {\displaystyle E_{av}={\frac {2}{\pi }}E_{m}} （交流電圧の平均値）、 I a v = 2 π I m {\displaystyle I_{av}={\frac {2}{\pi }}I_{m}} （交流電流の平均値）
※この「平均値」の解説は、「交流」の解説の一部です。
「平均値」を含む「交流」の記事については、「交流」の概要を参照ください。
平均値
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2021/10/22 22:27 UTC 版)
藏澄らの男女別の式を用いた日本人における平均体表面積は、男性：1.69m2、女性：1.51m2である。
※この「平均値」の解説は、「体表面積」の解説の一部です。
「平均値」を含む「体表面積」の記事については、「体表面積」の概要を参照ください。
「平均値」の例文・使い方・用例・文例
- 四分位間の平均値を求めなさい
- 周波数の平均値は振幅の増大にしたがって減じる。
- 図１中のグラフは各学年の白人と黒人の総計点の平均値の相違を示している。
- 定義された地域のいくつかの特質あるいは量の平均値を求めるため、段階的に違う影、色、内側のシンボルを使用している地図
- 分子のアセンブリにおける総エネルギーは、等しく分配されず、統計的分布に従い、平均値のあたりで分配される
- 2つの変量の個別の平均からの偏差の積の平均値
- 平均値における規則正しい周期的変動
- 身長・体重が同じ年齢の子供の平均値よりかなり低い子供
- (数学で)算術平均という平均値
- n個の数の和をnで割って得られる平均値
- 大潮の時の,潮差の平均値
- 平均値
- 相乗平均という平均値
- 過去30年間の気候の平均値
- 標準偏差と平均値との比
- 変量が平均値からずれる誤差をあらわす量
- 地球表面に入射する太陽エネルギーの大きさの平均値
平均値と同じ種類の言葉
「平均値」に関係したコラム
-
FXやCFDのRMI（Relative Momentum Index）とは、テクニカル指標のモメンタムを用いて、値動き幅から相場の売られ過ぎ、あるいは、買われ過ぎを判断するためのテクニカル指標のことで...
-
株式投資のスクリーニングとは、テクニカル指標や財務関連指標などを中心とした条件に合致した銘柄を抽出するシステムのことです。スクリーニングでは、テクニカル指標や財務関連指標の他に、投資金額や売買単位、業...
-
FXやCFDの三角形移動平均とは、移動平均の移動平均のことです。つまり、移動平均値を算出して、さらにその数値の移動平均値を算出します。なお、移動平均には単純移動平均を用います。三角形移動平均は、三角移...
-
テクニカル分析でバイナリーオプションの予想をするには、テクニカル指標によりその先の値動きを予測します。ここでは、いくつかのテクニカル指標と予想の仕方を紹介します。▼EMA（Exponential Mo...
-
FX（外国為替証拠金取引）のエンベロープ（envelope）とは、移動平均線を応用したテクニカル指標の1つです。エンベロープは、移動平均線を中心にして、上値と下値に平行線を描画します。そして、上値を超...
-
FXやCFDのDPO（Detrended Price Oscillator、ディトレンディドプライスオシレーター）とは、移動平均の乖離を用いたテクニカル指標のことです。DPOの計算方法は、まずn日間の...
- 平均値のページへのリンク
