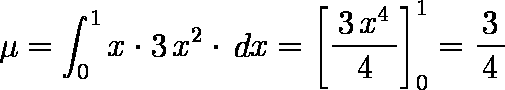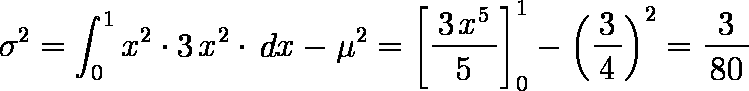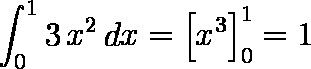例題
例題： 表 1 のデータについて標本平均，標本分散，母平均，母分散を求めなさい。
| 和xi | 度数 | 相対度数 | 累積相対度数 | 確率f(xi) | 分布関数F(xi) |
|---|---|---|---|---|---|
| 2 | 23 | 0.023 | 0.023 | 1/36=0.028 | 1/36=0.028 |
| 3 | 48 | 0.048 | 0.071 | 2/36=0.056 | 3/36=0.083 |
| 4 | 90 | 0.090 | 0.161 | 3/36=0.083 | 6/36=0.167 |
| 5 | 101 | 0.101 | 0.262 | 4/36=0.111 | 10/36=0.278 |
| 6 | 158 | 0.158 | 0.420 | 5/36=0.139 | 15/36=0.417 |
| 7 | 160 | 0.160 | 0.580 | 6/36=0.167 | 21/36=0.583 |
| 8 | 135 | 0.135 | 0.715 | 5/36=0.139 | 26/36=0.722 |
| 9 | 122 | 0.122 | 0.837 | 4/36=0.111 | 30/36=0.833 |
| 10 | 87 | 0.087 | 0.924 | 3/36=0.083 | 33/36=0.917 |
| 11 | 50 | 0.050 | 0.974 | 2/36=0.056 | 35/36=0.972 |
| 12 | 26 | 0.026 | 1.000 | 1/36=0.028 | 36/36=1.000 |
| 合計 | 1000 | 1.000 | 1.000 |
解： 1000 個の標本について，標本平均
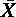，標本分散 V は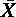， = ( 2 ・ 23 + 3 ・ 48 + 4 ・ 90 + 5 ・ 101 + 6 ・ 158 + 7 ・ 160 + 8 ・ 135 + 9 ・ 122 + 10 ・ 87 + 11 ・ 50 + 12 ・ 26 ) / 1000 =
7.033
V = ( 22 ・ 23 + 32 ・ 48 + 42 ・ 90 + 52 ・ 101 + 62 ・ 158 + 72 ・ 160
+ 82 ・ 135 + 92 ・ 122 + 102 ・ 87 + 112 ・ 50 + 122 ・ 26 ) / 1000 - 7.0332
= 5.569911
また，母平均 μ，母分散 σ2 は，
μ = 2 ・ 1 / 36 + 3 ・ 2 / 36 + 4 ・ 3 / 36 + 5 ・ 4 / 36 + 6 ・ 5 / 36 + 7 ・ 6 / 36
+ 8 ・ 5 / 36 + 9 ・ 4 / 36 + 10 ・ 3 / 36 + 11 ・ 2 / 36 + 12 ・ 1 / 36
= 7
σ2 = ( 22 ・ 1 / 36 + 32 ・ 2 / 36 + 42 ・ 3 / 36 + 52 ・ 4 / 36 + 62 ・ 5 / 36 + 72 ・ 6 / 36
+ 82 ・ 5 / 36 + 92 ・ 4 / 36 + 102 ・ 3 / 36 + 112 ・ 2 / 36 + 122 ・ 1 / 36 - 72
= 35 / 6
= 5.83333333
例題
例題
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2021/08/09 09:13 UTC 版)
ナビゲーションに移動 検索に移動| ウィキペディアには「例題」という見出しの百科事典記事はありません（タイトルに「例題」を含むページの一覧/「例題」で始まるページの一覧）。 代わりにウィクショナリーのページ「例題」が役に立つかも知れません。 |
|
例題
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2020/09/05 06:31 UTC 版)
無限に広がる真空中の誘電率を ε 0 = 1 {\displaystyle \varepsilon _{0}=1} 、電荷密度を ρ ( r ) {\displaystyle \rho (\mathbf {r} )} とするとき、静電ポテンシャル ϕ ( r ) {\displaystyle \phi (\mathbf {r} )} はポアソン方程式 Δ ϕ ( r ) = − ρ ( r ) {\displaystyle \Delta \phi (\mathbf {r} )=-\rho (\mathbf {r} )} を満たす。ただし Δ {\displaystyle \Delta } はベクトル解析における3次元ラプラシアンであり、 Δ = ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 + ∂ 2 ∂ z 2 {\displaystyle \Delta ={\dfrac {{\partial }^{2}}{\partial x^{2}}}+{\dfrac {{\partial }^{2}}{\partial y^{2}}}+{\dfrac {{\partial }^{2}}{\partial z^{2}}}} である。これを偏微分方程式とみなしてフーリエ変換を用いて解き、 ϕ ( r ) {\displaystyle \phi (\mathbf {r} )} を求めよ。
※この「例題」の解説は、「物理数学」の解説の一部です。
「例題」を含む「物理数学」の記事については、「物理数学」の概要を参照ください。
「例題」の例文・使い方・用例・文例
例題と同じ種類の言葉
- >> 「例題」を含む用語の索引
- 例題のページへのリンク
