中央値

新語時事用語辞典

中央値

読み方：ちゅうおうち
英語：median

中央値とは、中央値の意味

中央値とは、数値で構成された複数のデータを小さい順番に並べた時に、真ん中に位置する値のことである。数学や統計学の分野でよく使われる用語である。英語では median と表現される。

中央値は、例えば10から20までの整数がある場合、小さい方から6番目（あるいは大きい方から6番目）の数の15が中央値となる。

エクセル（Excel）で中央値を算出するには「MEDIAN関数」を使用する。例えば、A2セルからA10セルまでの数値の中央値を求めるには、「=MEDIAN(A2:A10)」とする。

中央値と平均値の違い

平均値とは、複数の数値の合計を、数値の個数で除した値のことである。エクセルでは、「AVERAGE関数」を使用する。例えば、A2セルが1、A3セルが2、A4セルが6の場合、「＝AVERAGE（A2:A4）」で求めることができる。平均値は 3 となる。ちなみに「＝MEDIAN（A2:A4）」とすると中央値として 2 が表示される。

（2020年8月18日更新）

デジタル大辞泉

ちゅうおう‐ち〔チユウアウ‐〕【中央値】

読み方：ちゅうおうち

資料を大きさの順に並べたとき、全体の中央にくる値。資料の個数が偶数のときは中央にある二つの値の平均値。中位数。メジアン。メディアン。

環境アセスメント用語集

中央値 (ちゅうおうち)

　測定値を大きさの順に並べたとき、その中央に当たる一つの値。または中央の二つの平均値。

L50値（中央値） (－ち)

　騒音計の指示値が不規則に変動する場合の騒音レベル表現の一つで、L50値はそのレベルより高いレベルの時間と低いレベルの時間が半分ずつあることを示す。

統計学用語辞典

中央値（Me）

　測定値を小さい順に並べたとき，ちょうど真ん中にくる値である。分布の両端に大きな値や小さな値があっても影響されない（注）。
　有効ケース数を n，各ケースの測定値を Xi （ i = 1，2，… ，n ）とすると，以下の式で定義される。

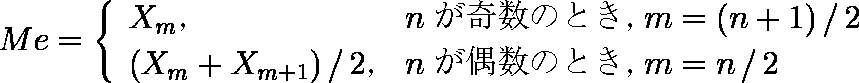
　例題：「6 人の身長が 156.8，168.7，163.8，154.1，159.6，165.6 であった。中央値を求めよ。」
　解答：小さい順に並べると，154.1，156.8，159.6，163.8，165.6，168.7 になる。m = 6 / 2 = 3 ゆえ，3 番目と 4 番目のデータの平均値が中央値 Me である。よって Me = ( 159.6 + 163.8 ) / 2 = 161.7 である。


One more step!
　しかし，同点があるときには上の式を直接使うと不適切な場合がある。
　例題： 22 個の測定値がある。中央値を求めよ。
　　　測定値：1，1，2，2，2，2，3，3，3，3，3，3，3，3，4，4，4，4，4，4，5，5
　解答：定義からいえば，中央値は 3 であるが，もう少しましな推定値を求めよう。

1. まずデータ整理のために度数分布表を作る。

   測定値	度数	相対度数	累積度数	累積相対度数
   1	2	9.1	2	9.1
   2	4	18.2	6	27.3
   3	8	36.4	14	63.6
   4	6	27.3	20	90.9
   5	2	9.1	22	100.0
   合計	22	100.0

   
   
2. 定義からいえば，中央値より小さいものは全体の 50%，大きいものは 50% あることになる。しかし，中央値 = 3 としたとき，3 より小さいものは 27.3%，大きいものは 36.4% あることになる。中央値は 3 以上，4 未満の値であるに違いない。
   
3. 測定値 3 を持つ 8 個のデータは 2.5 以上，3.5 未満に 1 / 8 =　0.125 の間隔で均等に分布しているとすると，8 個のデータのもっともらしい値は，2.500，2.625，2.750，2.875，3.000，3.125，3.250，3.375 である。この中の 5 番目と 6 番目のデータの真ん中の値が中央値である。すなわち，Me = ( 3.000 + 3.125 ) / 2 = 3.0625 となる。確かに 3.0625 より小さいデータは 11 個になることが確かめられる。
   注意：真の値が 2.5 以上，3.5 未満のとき，四捨五入されて測定値 3 が得られると考えるところがポイント。しかし，8 個のデータがその範囲に均等に分布する保証があるのか？とか，もっともらしい値が 2.500 から始まるのか？ということをつつけば問題もある。

　以上のことを一般化すると，以下のようになる。
　l を中央値のある級間の下限点，F を l 以下の累積度数，fm を中央値のある級間の度数，h を級間の幅として，比例配分により次式を得る。


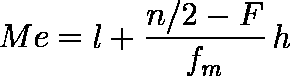
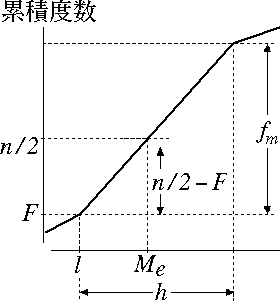
　例題では，n = 22，l = 2.5，F = 6，fm = 8，h = 1 ゆえ，Me = 3.125 となる。
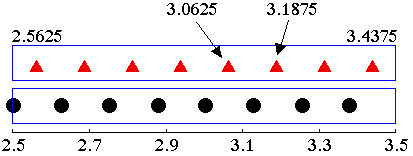
　注意：先の例では，Me = 3.0625 であった。これは，8 つの同値のデータが下図の●のように分布しているとしたものである。しかし，▲のように分布していると考える方が一般的かもしれない。このようにすると▲は●より 0.125/2 = 0.0625 大きい方向へずれている。従って，得られる中央値も，Me = (3.0625+3.1876)/2=3.125 となり，上式による結果と一致する。

人口統計学辞書

中央値（中位数、メディアン）

人口学でもっとも頻繁に用いられる平均 ¹は算術平均 ²であって、一連の指標に関する数量の合計をその生起回数で割った商から成っている。平均という言葉が何かの限定を付けずに用いられる場合は通常、算術平均を意味する。幾何平均 ³は、全観測値が正の場合に用いられることがある。これはN個の数値の積のN乗根である。加重平均 ⁴は個々の数量にそれぞれ違った特定の重み ⁵を乗ずることにより求められる。中央値（中位数、メディアン） ⁶は一組 ⁷の観測データを大きさの順に並べた時にちょうど中央に位置するデータの値である。最頻値（モード） ⁸は一連の観測値の中で最も普通でありよく用いられる値である。

• 1. 平均average（名）：形容詞としても用いることができる。
  平均mean（名）：形容詞としても用いることができる。
• 5. 重みweight（名）：加重する（重みづけする）weigh（動）。
• 6. 中央値（中位数、メディアン）median（名）（訳注）：形容詞としても用いることができる。
  （訳注）日本語の場合、名詞としては中央値、形容詞的用法としては中位数という言葉が用いられる傾向がある。たとえば、年齢中央値と中位数年齢は同じものを指す。
• 8. 最頻値（モード）mode（名）；最頻値のmodal（形）。

PDQ®がん用語辞書

中央値

【仮名】ちゅうおうち
【原文】median

統計用語。一連の測定値のうち中央にくる測定値。

ウィキペディア

中央値

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2024/10/31 02:10 UTC 版)

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。（このテンプレートの使い方） 出典検索?: "中央値" – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2023年11月)

この記事は英語版の対応するページを翻訳することにより充実させることができます。（2024年5月） 翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。 英語版記事を日本語へ機械翻訳したバージョン（Google翻訳）。 万が一翻訳の手がかりとして機械翻訳を用いた場合、翻訳者は必ず翻訳元原文を参照して機械翻訳の誤りを訂正し、正確な翻訳にしなければなりません。これが成されていない場合、記事は削除の方針G-3に基づき、削除される可能性があります。 信頼性が低いまたは低品質な文章を翻訳しないでください。もし可能ならば、文章を他言語版記事に示された文献で正しいかどうかを確認してください。 履歴継承を行うため、要約欄に翻訳元となった記事のページ名・版について記述する必要があります。記述方法については、Wikipedia:翻訳のガイドライン#要約欄への記入を参照ください。 翻訳後、{{翻訳告知|en|Median|…}}をノートに追加することもできます。 Wikipedia:翻訳のガイドラインに、より詳細な翻訳の手順・指針についての説明があります。

中央値（ちゅうおうち、英: median）あるいはメジアン、メディアンとは、データや集合の代表値の一つで、順位が中央である値のことである。ただし、データの大きさが偶数の場合は、中央順位2個の値の算術平均をとる。

例えば5人の年齢10歳、32歳、96歳、100歳、105歳からなるデータの中央値は、順位が上からも下からも3である96（歳）となる。0歳の子供が2人増えて7人になると、中央値は32歳となる。

平均値との関係

最頻値・中央値・平均値の図示

中央値は平均値と同様に集団の代表値を得る目的で使う。例えば年収からなるデータの場合を考えてみると分かりやすい。

一部の富裕層が平均年収をつり上げてしまう例を考える。人口100人の集落で、90人が年収200万円だとしても、10人が年収5000万円であれば平均年収は680万円となる。

一方中央値は、年収が低い順（高い順）に国民を並べたときに丁度真ん中になる人の年収を表している。この場合、中央値はあいかわらず200万円であり、一部の富裕層の年収が中央値に与える影響はゼロになる。

例えば一人の億万長者が小さな町に引っ越してくれば平均年収はつり上がってしまうが、年収の中央値はたかだか一順位分変わるに過ぎない。

厳密な定義

実確率変数 X の累積分布関数を F(x) とするとき、 F(x) は実数値非単調減少関数、右連続関数となる。この時、次の不等式を満たす実数 m を中央値（メディアン）と呼ぶ。

${\displaystyle \int _{-\infty }^{m}\mathrm {d} F(x)\geq {\frac {1}{2}}{\text{ and }}\int _{m}^{\infty }\mathrm {d} F(x)\geq {\frac {1}{2}}\,\!}$ カテゴリ