平均値の多重比較
平均値の多重比較は，いくつかの群の平均値に全体として差が見られたときに，どの群の間に差があるかを検定するための手法である。
 対比較 | ||
 ライアンの方法 | ||
| テューキーの方法 | ||
| 線形比較 | ||
| テューキーの方法 | ||
| シェッフェの方法 | ||
| 対照群との比較 | ||
| ダネットの方法 | ||
平均値の多重比較（対比較--ライアンの方法）
一元配置分散分析の結果，全体としての平均値に有意な差が認められたときにも，全ての群間に平均値の差があるわけではない。
対比較とは，どの 2 群の平均値の間に有意な差があるかを検定するための方法である。
例題：
「都道府県を 4 つに分けてそれぞれの群における癌による死亡率（人口 10 万人あたり）の集計結果は表 1 のようであった。平均値に差があるといえいるか，有意水準 5% で検定しなさい。また，多重比較を行いなさい。」
| 都道府県数 | 平均値 | 標準偏差 | |
|---|---|---|---|
| 第1群 | 8 | 135.83 | 19.59 |
| 第2群 | 11 | 160.49 | 12.28 |
| 第3群 | 22 | 178.35 | 15.01 |
| 第4群 | 6 | 188.06 | 9.81 |
| 全体 | 47 | 168.17 | 22.40 |
検定手順:
- 前提
- ライアンの方法では，名義的有意水準（α '）という概念が使われる。k 群の場合，全ての 2 群の平均値の差を検定する場合には，kC2 回の検定を行わなければならない。検定結果全体としての有意水準を α とするためには，個々の検定において有意水準を α / kC2 まで下げておけばよい。しかし，もし平均値の最大値と最小値に有意な差が認められたときには，次の段階で k - 1 個の平均値の差を検定するときには，有意水準をもう少し大きくしてもよいであろう。このように考えると，個々の検定に使用する有意水準として，次式で表される名義的有意水準を使用すればよい。
α' = 2 α / { k ( m - 1 ) }
ここで，m は比較する 2 個の平均値を
i，j としたとき，i ≧ p ≧ j を満たす p の個数である。
- i と j の平均値の差の検定には，次式による t0 統計量を用いる。ここで，Vw は群内平均平方（群内分散），ni，nj は群 i，群 j のケース数である。
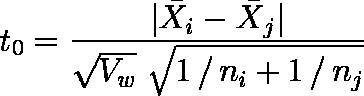
- t0 統計量は，自由度が n-k（すなわち Vw の自由度と同じ。）の t 分布に従う。
- 有意確率を P = Pr｛｜t｜≧ t0｝ とする。
- 帰無仮説の採否を決める。
対比較は，以下のように行われる。
- まず，平均値が最大である群と，最小である群について検定を行う。
このとき，m = k である。もし有意差なしならば，検定終了。結論は「個々の平均値対に差はない」とする。
もし有意差ありならば，次へ進む。
- m = k - 1 となるような 2 個の平均値の比較を行う。このような平均値の組合せは 2 通りある。すなわち，最大の平均値 vs. 2 番目に小さい平均値，2 番目に大きい平均値 vs. 最小の平均値の検定を行うことになる。
名義的有意水準は，1. の場合よりも大きくなる。
- m = k - 2， k - 3， ... ，2 となるような 2 個の平均値の比較を行う。ここで注意すべきことは，対象となる 2 個の平均値が，それまでの検定実施の過程で有意差なしとされた平均値に挟まれている場合には，検定を実施せずにただちに有意差なしと結論する。例えば，a ≧ b ≧ c ≧ d （a = b または c = d の場合を含む）で，a 群と d 群の平均値に有意差がなかったとしたら，無条件に a：b，a：c，b：c，b：d，c：d 群にも平均値に有意差がないとする。これは，前述の 1. の検定結果に対する解釈規定と同じである。
以上のようにして得られた全ての結論，すなわち「群 x と群 y，群 u と群 v ... に平均値の差が認められた。そのほかの平均値の組合せには有意差は認められなかった」は，全体としての有意水準が α になる。
例題の解：
| 比較する群 | 名義的有意水準 | t 値（Ryan） | 自由度 | 有意確率 |
|---|---|---|---|---|
| 第 4 群：第 1 群 | 0.00833333 | 6.538662 | 43 | ＜0.0000001 |
| 第 4 群：第 2 群 | 0.01250000 | 3.672794 | 43 | 0.0006595 |
| 第 3 群：第 1 群 | 0.01250000 | 6.963078 | 43 | ＜0.0000001 |
| 第 3 群：第 2 群 | 0.02500000 | 3.269975 | 43 | 0.0021219 |
| 第 2 群：第 1 群 | 0.02500000 | 3.588144 | 43 | 0.0008472 |
平均値の多重比較（対比較--テューキーの方法）
本来は各群の例数の等しい場合をテューキーの方法と呼び，例数が等しくない場合に拡張したものをテューキー・クレーマーの方法と呼ぶことが多い。
古い本には，「各群の例数が等しくない場合にはテューキー・クレーマーの方法は使えない」と書いてあるが，現在（1984年以降）では「対比較を行う場合にはテューキー・クレーマーの方法を使うべきである」ということになっている。
例題：
「都道府県を 4 つに分けてそれぞれの群における癌による死亡率（人口 10 万人あたり）の集計結果は表 1 のようであった。各群の平均値の全ての組み合わせに対して対比較を行いなさい。」
| 都道府県数 | 平均値 | 標準偏差（注） | |
|---|---|---|---|
| 第1群 | 8 | 135.83 | 19.59 |
| 第2群 | 11 | 160.49 | 12.28 |
| 第3群 | 22 | 178.35 | 15.01 |
| 第4群 | 6 | 188.06 | 9.81 |
| 全体 | 47 | 168.17 | 22.40 |
検定手順:
- 前提
- 誤差分散 Vw = （一元配置分散分析における群内不偏分散と同じ）を計算する。
- 全ての 2 群の組み合わせについて検定統計量を計算する。
第 i 群と第 j 群（i ＜ j）の平均値をそれぞれi，j，サンプルサイズを ni，nj とすると，検定統計量 tij は次の式で計算される。
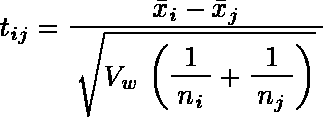
- “ステューデント化した範囲の表”（α = 0.05，α = 0.01）から，「群の数」が k，自由度ν（誤差分散 Vw に対応する自由度。すなわち，一元配置分散分析における群内不偏分散の自由度と同じ）に対応する数値を読みとり，この値を q(k,ν,α) とする。
なお，対応する自由度が表にない場合には，もよりの 2 個の自由度に対する値から自由度の逆数補間で求める。
- 比較する群間に平均値の差があるかどうか判断する。
例題の解：
- 誤差分散 Vw = { (8-1)×19.562+(11-1)×12.282+(22-1)×15.012+(6-1)×9.812 } / (47-4) = 9406.8433 / 43 = 218.7638。
対応する自由度 ν は 47-4 = 43。
- 検定統計量 tij は以下の通り。
表 2．47 都道府県における癌死亡率に対するテューキーの方法による検定統計量 j＼i 第 1 群 第 2 群 第 3 群 第 2 群 3.588* 第 3 群 6.963* 3.270* 第 4 群 6.593* 3.673* 1.425
- 群の数（k）= 4，ν = 43 のときの3.779 q(k,ν,α) は，“ステューデント化した範囲の表”（α = 0.05）にないので，補間する。
νb = 43，νa = 40，νc = 60，a = 3.79，c = 3.74 として，逆数補間 により，νb = 43 のときの q(k,ν,α) は 3.779534884 である。
- q(k,ν,α) /√2 = 2.672534746 と表の検定統計量を比較する。有意な差が認められるものに * をつけておく。
- 平均値の多重比較のページへのリンク
