線形比較--シェッフェの方法
線形比較によれば，平均値のあらゆる比較ができる。
線形比較とは，次式で表される θ である。
θ = c1 μ1 + c2 μ2 + … + ck μk
ただし，c1 + c2 + … + ck = 0
例えば，全体で 5 群あり，第 1，2，3 群をこみにしたものと第 4，5 群をこみにしたものの比較の場合には，
c1 = c2 = c3 = 1 / 3，c4 = c5 = -1 / 2
とする。
得られる平均値の線形結合値の信頼区間を求め，信頼区間に 0 が含まれない場合には，プールした 2 群の平均値に差があるとする。
なお，対比較も，ci = 1，cj = -1，ca = 0（a ≠ i，j）のようにすれば可能であるが，検出力は対比較の方が高い。
事前にまとめる群が決まっている場合には t 検定でもよいが，結果をみてから検定を行う場合には線形比較によらなければならない。
群のケース数は等しくなくてもよい。
例題：
「都道府県を 4 つに分けてそれぞれの群における癌による死亡率（人口 10 万人あたり）の集計結果は表 1 のようであった。平均値に差があるといえいるか，有意水準 5% で検定しなさい。また，多重比較を行いなさい。」
| 都道府県数 | 平均値 | 標準偏差 | |
|---|---|---|---|
| 第1群 | 8 | 135.83 | 19.59 |
| 第2群 | 11 | 160.49 | 12.28 |
| 第3群 | 22 | 178.35 | 15.01 |
| 第4群 | 6 | 188.06 | 9.81 |
| 全体 | 47 | 168.17 | 22.40 |
検定手順:
- 前提
- 線形比較の推定値
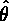を次式により求める。
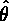= c1 
1 + c2 2 + … + ck k
ただし，c1 + c2 + … + ck = 0
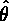- の分散を次式により求める。
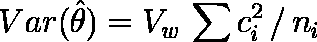
- 第 1 自由度が dfb（ = k - 1 ），第 2 自由度が dfw（ = n - k ）である F 分布の
上側 α パーセント点を F0 とする。
F 分布表（α = 0.05，α = 0.025，α = 0.01，α = 0.005），または F 分布のパーセント点の計算を参照すること。
- θ の信頼限界を次式により求める。
- 帰無仮説の採否を決める。
全ての可能な線形比較の結果は，指定された有意水準のもとで正しい（全ての可能な線形比較をした場合には，この方法は，一元配置分散分析検定と等価である。）。
4 以降の手順は以下のようにしてもよい。
- 次式で F0 検定統計量を求める。
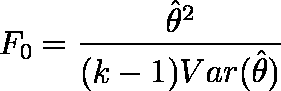
- 検定統計量 F0 は，第 1 自由度が dfb（ = k - 1 ），第 2 自由度が dfw（ = n - k ）の F 分布に従う。
- 第 1 自由度が dfb，第 2 自由度が dfw の F 分布において，有意確率を P = Pr｛F ≧ F0｝ とする。
F 分布表（α = 0.05，α = 0.025，α = 0.01，α = 0.005），または F 分布の上側確率の計算を参照すること。
- 帰無仮説の採否を決める。
例題の解：
- 一元配置分散分析の結果，全体として平均値の差があることがわかる。
- 群内分散 Vw = 218.763798，その自由度は 43 である。
- 第 1，2 群をプールした平均値と，第 3，4 群をプールした平均値の差の検定を行うときは，c1 = c2 = 0.5，c3 = c4 = -0.5 とする。
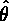- ＝-35.045 となる。
- Var(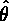) = 23.4093837 となる。
- 自由度（3，43）のF 分布において，上側確率が 5% となるパーセント点は 2.82162915 である。
- θ の信頼区間は [ -49.12185 , -20.96815 ] となり，0 を含まないので，平均値に差があるとする。
- 別法では，F0 = 17.4880302 となり，これが自由度（3，43）のF 分布に従うので，P = Pr｛F ＞ 17.4880302｝＜ 0.0001 ゆえ，5 % の有意水準で平均値に差があるとする。
- 多重比較の結果（一部分）は以下のようになる。
| 比較する群 | 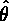| 信頼区間 | F 値 | 自由度 | 有意確率 |
|---|---|---|---|---|---|
| （1，2）：（3，4） | -35.04500 | ［ -49.12185 ，-20.96815 ］ | 17.4880302 | （ 3，43 ） | 0.0000001 |
| （1，2，3）：（4） | -29.83667 | ［ -48.87380 ，-10.79954 ］ | 6.9310236 | （ 3，43 ） | 0.0006583 |
| （2，3）：（4） | -18.64000 | ［ -37.92121 ，0.6412072 ］ | 2.6370791 | （ 3，43 ） | 0.0616931 |
線形比較--テューキーの方法
線形比較によれば，平均値のあらゆる比較ができる。
線形比較とは，次式で表される θ である。
θ = c1 μ1 + c2 μ2 + … + ck μk
ただし，c1 + c2 + … + ck = 0
例えば，全体で 5 群あり，第 1，2，3 群をこみにしたものと第 4，5 群をこみにしたものの比較の場合には， c1 = c2 = c3 = 1 / 3，c4 = c5 = -1 / 2 とする。得られる平均値の線形結合値の信頼区間を求め， 信頼区間に 0 が含まれない場合には，プールした 2 群の平均値に差があるとする。
なお，対比較も，ci = 1，cj = -1，ca = 0（a ≠ i，j）のようにすれば可能であるが，検出力は対比較の方が高い。
事前にまとめる群が決まっている場合には t 検定でもよいが，結果をみてから検定を行う場合には線形比較によらなければならない。
例題：
「5 種類の飼料で飼育した魚の体長の平均値が表 1 のようであった。平均値に差があるといえいるか，有意水準 5% で検定しなさい。また，多重比較を行いなさい。」
| 匹数 | 平均値 | 不偏分散 | |
|---|---|---|---|
| 第 1 群 | 20 | 35.6 | 5.6 |
| 第 2 群 | 20 | 32.7 | 4.6 |
| 第 3 群 | 20 | 29.4 | 4.9 |
| 第 4 群 | 20 | 27.9 | 3.7 |
| 第 5 群 | 20 | 25.7 | 2.5 |
| 全体 | 100 | 30.26 | 16.53 |
検定手順:
- 前提
- 線形比較の推定値を次式により求める。
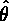= c1 1 + c2 2 + … + ck k
ただし，c1 + c2 + … + ck = 0
- θ の信頼限界を次式により求める。
ここで用いる q は，検定に使用する有意水準に対応する“ステューデント化した範囲の表”（α = 0.05，α = 0.01）での，群の数および Vw（群内分散）の自由度に対する値である。なお，対応する自由度が表にない場合には，もよりの 2 個の自由度に対する値から，自由度の逆数で比例配分して求める。
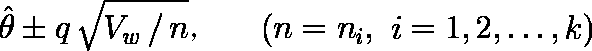
- 帰無仮説の採否を決める。
全ての可能な線形比較の結果は，指定された有意水準のもとで正しい。
例題の解：
- 一元配置分散分析の結果，全体として平均値の差があることがわかる。
F0 = 72.26761，自由度 = （4，95），有意確率 P ＜ 0.0001。
- 群内分散 Vw = 4.26，その自由度は 95 である。
- “ステューデント化した範囲の表”の，自由度60のときの 3.98 と，自由度 120 のときの 3.92 を用いて，自由度の逆数で比例配分して求めると q = 3.93579 である（正確な値は 3.932736）。
- 第 1，2，3 群をプールした平均値と，第 4，5 群をプールした平均値の差の検定を行うときは，c1 = c2 = c3 = 1/3，c4 = c5 = -0.5 とする。
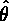- ＝5.766667 となる。
- θ の信頼区間は [ 3.950224 , 7.583109 ] となり，0 を含まないので，母平均値に差があるとする。
- 多重比較の結果（一部分）は以下のようになる。
| 比較する群 | | 信頼区間 | 判定 |
|---|---|---|---|
| （1，2，3）：（4，5） | 5.766667 | ［ 3.950224 ，7.583109 ］ | 有意な差である |
| （1，2）：（4，5） | 7.350000 | ［ 5.533557 ，9.166443 ］ | 有意な差である |
| （1）：（4，5） | 8.800000 | ［ 6.983557 ，10.61644 ］ | 有意な差である |
| （2，3）：（4，5） | 4.250000 | ［ 2.433557 ，6.066443 ］ | 有意な差である |
線形比較と同じ種類の言葉
- 線形比較のページへのリンク
