群ごとの平均値・不偏分散を統合する方法
例題:
「表 1 のように,4 群のサンプル数,平均値,標準偏差(不偏分散の平方根)が計算されている。これから,全体の(4 群をこみにした)平均値,標準偏差を求めなさい。」
| 都道府県数 | 平均値 | 標準偏差 | |
|---|---|---|---|
| 第1群 | 8 | 135.83 | 19.59 |
| 第2群 | 11 | 160.49 | 12.28 |
| 第3群 | 22 | 178.35 | 15.01 |
| 第4群 | 6 | 188.06 | 9.81 |
計算手順:
- 群の数が k の場合に,群ごとの有効ケース数 ni,平均値
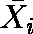 ,不偏分散 Ui(i=1,2,... ,k)が求められているとする。定義式は以下の通り。
,不偏分散 Ui(i=1,2,... ,k)が求められているとする。定義式は以下の通り。
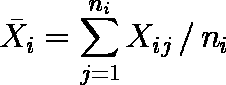
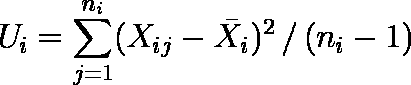
- 全群をこみにした有効ケース数 nt は,次式で求められる。
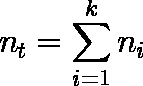
例題では,nt = 8 + 11 + 22 + 6 = 47
- 全群をこみにした平均値
 は,次式で求められる。
は,次式で求められる。
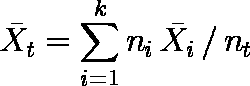
例題では, = ( 8・135.83 + 11・160.49 + 22・178.35 + 6・188.06 ) / 47 ≒ 168.17212
= ( 8・135.83 + 11・160.49 + 22・178.35 + 6・188.06 ) / 47 ≒ 168.17212
- 全群をこみにした不偏分散 Ut は,次式で求められる。
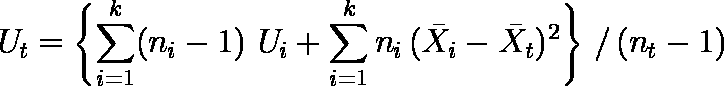
表 1 には標準偏差が与えられていることに注意して,例題では Ut = { 7・19.592 + 10・12.282 + 21・15.012 + 5・9.812 + 8・( 135.83 - 168.17212)2 + 11・( 160.49 - 168.17212)2 + 22・( 178.35 - 168.17212)2 + 6・( 188.06 - 168.17212)2 } / 46 = 501.657385
よって,全群をこみにしたときの標準偏差は 501.657385 の平方根をとって 22.3977094 である。
R による計算例
> n <- c(8, 11, 22, 6) > M <- c(135.83, 160.49, 178.35, 188.06) > SD <- c(19.59, 12.28, 15.01, 9.81) > U <- SD^2 > nt <- sum(n) > Mt <- sum(n*M)/nt > Ut <- (sum((n-1)*U)+sum(n*(M-Mt)^2))/(nt-1) > SDt <- sqrt(Ut) > cat(nt, Mt, Ut, SDt, sep=", ") 47, 168.1721, 501.6574, 22.39771 関数にすると > func <- function(n, M, U) + { + nt <- sum(n) + Mt <- sum(n*M)/nt + Ut <- (sum((n-1)*U)+sum(n*(M-Mt)^2))/(nt-1) + SDt <- sqrt(Ut) + cat(nt, Mt, Ut, SDt, sep=", ") + } > n <- c(8, 11, 22, 6) > M <- c(135.83, 160.49, 178.35, 188.06) > SD <- c(19.59, 12.28, 15.01, 9.81) > func(n, M, SD^2) 47, 168.1721, 501.6574, 22.39771
- 群ごとの平均値・不偏分散を統合する方法のページへのリンク
