補足説明

実用日本語表現辞典

補足説明

読み方：ほそくせつめい

説明の十分でない箇所について追加で説明すること。説明を加えて補うこと。物事の背景や事情、経緯、その他の参考情報などが補足説明として言及されることが多い。

（2011年10月31日更新）

統計学用語辞典

補足説明

1. ステップワイズ変数選択によって得られた判別関数に，必要な変数が入っていない，あるいは不要な変数が入っているということが生ずる場合がある。後者の場合には最初から不要な変数を除去すればよいのであるが，前者の場合には若干の問題がある。「必要な変数」であるとした判断基準が明確ならば，判別関数を構成したい変数のセットを指定して，ステップワイズ変数選択をしないで分析する。判断基準が明確でない場合には，なぜその変数が選ばれなかったかをよく検討する必要がある。手元にあるケースが母集団を代表し得るか，他の重要な説明変数が抜けているために副作用的に選ばれなかったのではないかなど。
   
2. 得られた判別関数を実地へ適用する場合には，判別関数の計算が簡便になるように判別関数に含まれる変数の数が少ないことや，群の数が多い場合には各群の判別に使用する判別関数の数が少ないほうが都合がよいであろう。3 群以上の判別には 正準判別分析 を使用することによって，少数個の判別関数で群の判別が可能であろう。
   
3. 得られた判別関数は，分析に使用したケースについて最適のものであるが，別のケース群に適用しても有用であるかどうかはわからない。例えば，ある医療機関に受療した患者に適用できても，別の医療機関の受療患者には適用できないかもしれない。得られた判別関数が他の集団でも有用であるかどうか（ 交差妥当性 を持つかどうか ）について検討したほうがよい。
   
4. 交差妥当性を検証するのはなかなかたいへんな場合がある。そのため，便法として 折半法 と呼ばれる方法がある。この方法は，既存のケースを無作為に半分ずつに分け，一方のケースを用いて判別関数を作り，もう一方のケースを得られた判別関数で判別し正判別率を検討するものである。折半法を用いるには，既存のケース数がある程度多くなければならない。
   
5. 判別分析は重回帰分析と密接な関連がある。二群の判別の場合，図のように従属変数を定義して重回帰分析を行うことにより，判別分析と同じ結果が得られる。
   

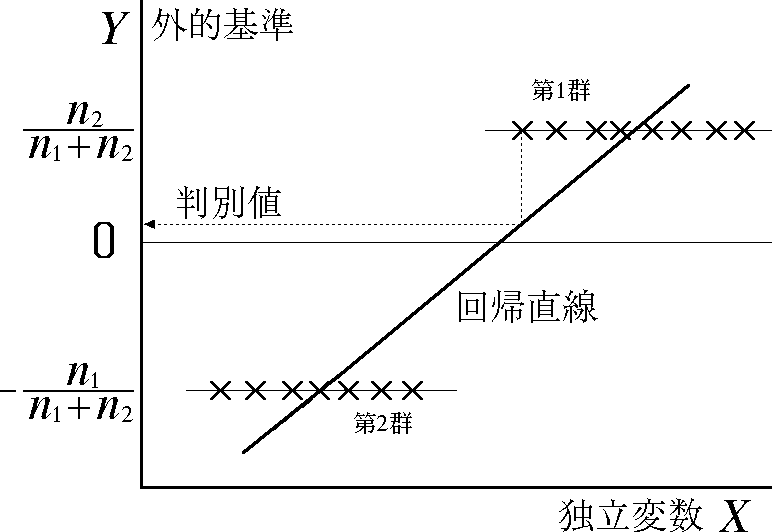
   判別分析と重回帰分析の関連

補足説明

1. 得られた主成分分析の結果が，常に解釈可能（ 既知の知見と整合性がある ）とは限らない。このような原因としては，既知の知見が不十分なために分析結果が正当に評価できない場合もあるし，分析に使用した変数のセットが不適切な場合（ 実態を把握するために必要な変数が抜け落ちているなど ）もあるであろう。
   
2. 得られた各ケースに対する主成分得点は総合特性値であるので，別の分析にも使用できる（ 各主成分の解釈が可能であれば妥当性が高くなる。解釈不十分でも限界はあるが可能 ）。例えば，クラスター分析の場合に，もとのデータを用いるかわりに少数個の主成分得点を使用することができる。
   
3. 得られた主成分の個数が多い場合には，例えば 2 組の主成分の組み合わせでケースのプロットをしても全容が把握しにくい。このような場合には，主成分得点を用いてクラスター分析を行ってみるのもよいであろう。

補足説明

• 得られた因子分析の結果が，常に解釈可能（ 既知の知見と整合性がある ）とは限らない。このような原因としては，既知の知見が不十分なために分析結果が正当に評価できない場合もあるし，分析に使用した変数のセットが不適切な場合（ 実態を把握するために必要な変数が抜け落ちているなど ）もあるであろう。
  
• 得られた各ケースに対する因子得点は，別の分析にも使用できる（ 各因子の解釈が可能であれば妥当性が高くなる。解釈不十分でも限界はあるが可能 ）。例えば，クラスター分析の場合に，もとのデータを用いるかわりに少数個の因子得点を使用することができる。
  
• 得られた因子数が多い場合には，例えば 2 組の因子の組み合わせでケースのプロットをしても全容が把握しにくい。このような場合には，因子得点を用いてクラスター分析を行ってみるのもよいであろう。

補足説明

1. 重回帰分析では，個々の説明変数は従属変数と直線相関関係にあることが仮定されている。個々の独立変数と従属変数の組合せで散布図を描き，直線相関から大幅にずれる独立変数は適当な変数変換をしてから用いた方がよい場合もある。
   
2. ステップワイズ変数選択によって独立変数の候補から自動的に重回帰式に取り入れる場合には，理論的に妥当な変数が必ずしも選択されないという不都合が生じる場合も多い。このような場合にはステップワイズ変数選択の結果を参考にして，変数選択を行わないで分析するのがよい。
   
3. 各変数が予測にどの程度寄与しているかを判断するためには，標準化偏回帰係数を見なければならない。
   
4. 回帰の分散分析の検定結果がどうであろうと，得られた予測式が実質的に有用かどうかの判断は，自由度調整済みの重相関係数の 2 乗に基づかなければならない。この値が 0.7 〜 0.8 程度以上でなければ，予測には役立たないであろう。このような場合には，従属変数を説明できる重要な変数が抜け落ちていないか検討する必要がある。
   
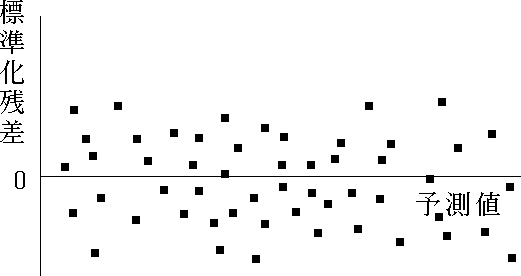
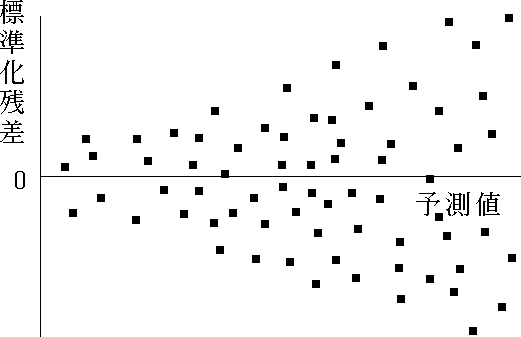
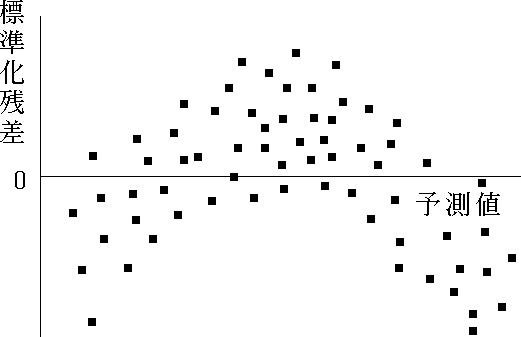
5. 予測値と標準化残差のプロット（ 残差分析 ）により，重回帰モデルの妥当性が検証できる。
   
   • 図 1 のように，予測値の大小にかかわらず標準化残差が一様に散らばっていれば重回帰モデルは妥当である。
     

     図 1．

     
     
   • 図 2 のように，データの中に外れ値がある場合には，数個の点が飛離れた位置にプロットされる。
     

     図 2．

     
     
   • 図 3 のように，予測値が大きく（ 小さく ）なるにつれ標準化残差の大きさが変化するような場合には分散が不均一であり，重回帰モデルが妥当でないことを表している。
     

     図 3．

     
     
   • 図 4 のように，標準化残差が曲線的な変動を見せるときは，独立変数と従属変数が曲線相関を示すので，なんらかの変数変換が必要であることを表す。
     

     図 4．

ウィキペディア小見出し辞書

補足説明

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2022/04/30 15:47 UTC 版)

「リトル・チャロ2」の記事における「補足説明」の解説

アニメの放送時間変更は、2011年（平成23年）7月24日に迫ったテレビの完全デジタル化に伴う恒常的なNHKのテレビコンテンツ抜本見直し、および『坂の上の雲』第2部放送開始によるミニ番組編成のため実施されたもの。

補足説明

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2015/01/23 20:36 UTC 版)

「実録漫画」の記事における「補足説明」の解説

日記漫画：作者の日常の出来事を描いた作品。 人物伝：実在のスポーツ選手の成長物語などの作品。 企画物：漫画のために何らかのイベントを実施したり、既存のイベントに参加する内容の漫画。 回顧録：漫画家本人による、過去を回想した作品。 この項目は、漫画に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています（P:漫画/PJ漫画/PJ漫画雑誌）。項目が漫画家・漫画原作者の場合には{{Manga-artist-stub}}を貼り付けてください。

補足説明

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2021/12/18 03:42 UTC 版)

「バプテスト教会」の記事における「補足説明」の解説

バプテスト派の教会は、この日本では特定の教派に属さない単立教会や、日本福音教会加盟教会のように聖霊派の教会[要出典]もある。 バプテスト派の教会の中には、日本バプテスト連合などのように「聖書にある初代教会（原始教会）の正統な継承者はバプテストである」と主張し、自らをプロテスタントの一派と位置づけない教会や教団も少数ながらある（ランドマーク・バプテスト）。 セブンスデー・アドベンチスト（SDAキリスト教会）も、米国バプテスト教会の流れにあり、かつては「セブンスデー・バブテスト」を名乗っていた。かつてはプロテスタント運動とは無関係という立場で一線を画していたが、現在ではプロテスタントの一派であると位置づけ穏健路線をとっている。

Weblio日本語例文用例辞書

「補足説明」の例文・使い方・用例・文例

• 補足説明ですが、ご提案金額は税抜き価格となっております。
• それについての補足説明をします。
• 私は次の3点に関し補足説明をした。
• 私はそれについて補足説明をする。
• 私はそれの補足説明をします。
• 私にそれの補足説明をさせて下さい。
• 彼の意見に補足説明をします。