不偏分散

統計学用語辞典

不偏分散 unbiased estimate of population variance

　母分散 σ^2 の推定量として S^2=Σ (Xi-Xbar)^2/n を使用したとき，S^2 は母分散の不偏推定量ではない。n 個の観察値は全体として自由度 n を持つが， Σ (Xi-Xbar)^2 は Xbar=Σ Xi/n という制約条件が 1 つあるので，自由度は n-1 になる。不偏分散が Σ(Xi-Xbar)^2/(n-1) のように n-1 で割られるのはここに起因する。不偏分散は（変動/自由度）で定義され，分散分析でも使用される（分散分析では，平均平方 mean square とも呼ばれる）。
詳しくは，不偏分散を参照のこと。

不偏分散（U）

　観測値の散らばりを表すと同時に，その観測値がえられた母集団における散らばりの推定値でもある（“母分散の不偏推定値”という）。
　有効ケース数を n，各ケースの測定値を Xi （ i = 1，2，… ，n ）とすると，以下の式で定義される。

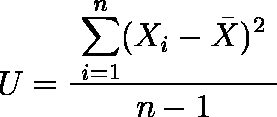
　すなわち変動を n-1 で割ったものである。分母が n - 1 であることに注意。ケース数が大きくなれば，分散と不偏分散の違いは小さくなる。
　上式を変形すると，次式が得られる。

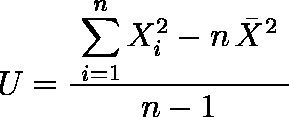
　この式は電卓などを用いて計算するときには便利なものであるが，コンピュータを用いて計算する場合には使わない方がよい。
　例題：5 つの測定値，2，3，4，7，9 の不偏分散を求めよ。
　解答：算術平均値は 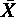= ( 2 + 3 + 4 + 7 + 9 ) / 5 = 5
　 不偏分散は U = { ( 2 - 5 )² +( 3 - 5 )² +( 4 - 5 )² +( 7 - 5 )² +( 9 - 5 )² } / ( 5 - 1 ) = { 3² + 2² + 1² + 2² + 4² } / 4 = 8.5
　 または，U = { 2² + 3² + 4² + 7² + 9² - 5・5² } / ( 5 - 1 ) = ( 159 - 125 ) / 4 = 8.5


　度数分布表から分散を求めるには，各階級の度数を fi，その中心点を Xi，m を階級数として，以下のように定義できる。

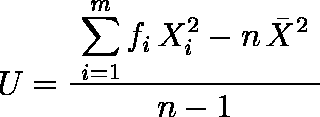
　例題：「426 人の女子学生の身長の度数分布が表 1 のようであった。不偏分散を求めよ。」

表 1．女子学生の身長の度数分布

階級（単位 cm）	度数
140 以上 145 未満	4
145 以上 150 未満	19
150 以上 155 未満	86
155 以上 160 未満	177
160 以上 165 未満	105
165 以上 170 未満	33
170 以上 175 未満	2
合計	426

　解答：以下のような計算表を作る。

中心点(Xi)	fi	fi・Xi	Xi2	fi・Xi2
142.5	4	570.00	20306.25	81225.00
147.5	19	2802.50	21756.25	413368.75
152.5	86	13115.00	23256.25	2000037.50
157.5	177	27877.50	24806.25	4390706.25
162.5	105	17062.50	26406.25	2772656.25
167.5	33	5527.50	28056.25	925856.25
172.5	2	345.00	29756.25	59512.50
合計	426	67300.00		10643362.50

算術平均値は 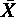= 67300 / 426 = 157.981221
不偏分散は U = ( 10643362.50 - 426・157.981221² ) / ( 426 - 1 ) = 26.4149406

日本酒用語集

不偏分散（ふへんぶんさん）

測定値のバラツキの物差し。すなわち変数のチラバリ（分布）の代表値として、次式による不偏分散s2を用いる。ただし、xiは個々の測定値、nは測定値の総数ある。