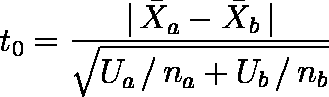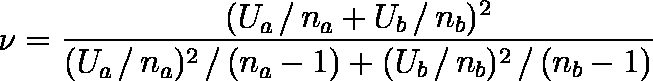二群の平均値の差の検定

統計学用語辞典

二群の平均値の差の検定（t 検定）

例題：
　「ある知能テストは，各種集団に実施したとき，平均値は変動するが，同じ年齢のものに適用する限り他の要因にかかわりなく，分散は同じであることが経験的にわかっている。いま 2 群に対して実施した結果，a 群 36 名の平均得点は 82.6 点，不偏分散は 15.3，b 群 43 名の平均得点は 84.5，不偏分散は 16.2 であった。2 群の母平均得点に差があるかどうか，有意水準 5% で両側検定しなさい。」


R による解析：

> my.t.test(36, 82.6, 15.3, 43, 84.5, 16.2, v=T)	# この関数の定義を見る
$method
[1] " Two Sample t-test"

$result
    t value       d. f.     P value 
 2.11651800 77.00000000  0.03753134 

二群の平均値の差の検定（t 検定）

例題：
　「ある地区で行った 40 歳以上 65 歳未満の住民検診に来所した男子 42 名，女子 63 名の血色素量についての検査成績は，男子では平均値 15.2 g/dl，不偏分散 1.1，女子では平均値 12.7 g/dl，不偏分散 3.2 であった。男女の平均値に差はあるか，有意水準 5% で両側検定しなさい。」


R による解析：

> my.t.test(42, 15.2, 1.1, 63, 12.7, 3.2, v=F)	# この関数の定義を見る
$method
[1] "Welch Two Sample t-test"

$result
     t value        d. f.      P value 
9.010303e+00 1.015811e+02 1.296324e-14 

二群の平均値の差の検定（t 検定）

例題：
　「ある知能テストは，各種集団に実施したとき，平均値は変動するが，同じ年齢のものに適用する限り他の要因にかかわりなく，分散は同じであることが経験的にわかっている。いま 2 群に対して実施した結果，a 群 36 名の平均得点は 82.6 点，不偏分散は 15.3，b 群 43 名の平均得点は 84.5，不偏分散は 16.2 であった。2 群の母平均得点に差があるかどうか，有意水準 5% で両側検定しなさい。」


検定手順：

1. 前提
   • 帰無仮説 H0：「2 群の母平均値に差はない」。
   • 対立仮説 H1：「2 群の母平均値に差がある」。
   • 有意水準 α で両側検定を行う（片側検定も定義できる）。
   
   
2. 記号の定義
   a 群，b 群のケース数を na，nb，平均値を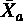 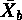，，不偏分散を ua，ub とする。
   例題では， na = 36，nb = 43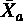， = 82.6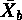， = 84.5，ua = 15.3，ub = 16.2 である。
   
3. 2 群の分散が等しいかどうかで，以下のいずれかを行う。
   例題では，「分散は同じであることが経験的にわかっている」ので通常の t 検定を行う。
   
   • 通常の t 検定
     2 群の分散が等しいと仮定できる場合，または，等分散性の検定で帰無仮説が採択された場合
     
     1. 二群をプールした分散の推定値 ue を次式により計算する。
        
        例題では，Ue = [ ( 36 - 1 ) 15.3 + ( 43 - 1 ) 16.2 ] / ( 36 + 43 - 2 ) = 15.79091 である。
        
     2. 検定統計量 t0 を次式により計算する。
        
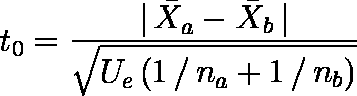
        例題では， t0 = 2.1165 である。
        
     3. t0 は自由度が ν = na + nb - 2 の t 分布に従う。
        例題では，ν = 77 である。
     
     
   • Welch の方法による t 検定
     2 群の等分散性が疑わしい場合，または，等分散性の検定で帰無仮説が棄却された場合
     
     1. 検定統計量 t0 を次式により計算する。
        
        
     2. t0 は自由度が ν の t 分布に従う。
        注：上式の ν は整数値にならないので，補間法により t0 の有意確率を求める。
        別法としては以下のようにすればよい。小数点以下を切捨てた自由度に対するパーセント点を tL としたとき，t0 ＞ tL ならば帰無仮説を棄却する。小数点以下を切上げた自由度に対するパーセント点を tU としたとき，tU ＞ t0 ならば帰無仮説を採択する。tL ＞ t0 ＞ tU のときは tL，tU から補間法によってパーセント点 tX を求め，tX ≦ t0 なら帰無仮説を棄却，tX ＞ t0 なら帰無仮説を採択する。
   
   
4. 有意確率をP = Pr｛｜t｜≧ t0｝とする。
   t 分布表，または t 分布の上側確率の計算を参照すること。
   例題では，t (77，0.05) ＜ t (60，0.05) = 2.00 ＜ t0 であるから，P ＜ 0.05 である（正確な有意確率：P = 0.03753）。
   
5. 帰無仮説の採否を決める。
   
   • P ＞ α のとき，帰無仮説を採択する。「2 群の母平均値に差があるとはいえない」。
   • P ≦ α のとき，帰無仮説を棄却する。「2 群の母平均値に差がある」。
   
   例題では，有意水準 5% で検定を行うとすれば（α = 0.05），P ＜ α であるから，帰無仮説を棄却する。すなわち，「母平均値に差がある」。

いくつかの注意点