二群の平均値の差の検定のとき

統計学用語辞典

二群の平均値の差の検定のとき

　有意水準 α，検出力 １−β で二群の平均値の差の検定を行うときに必要な標本の大きさを求める。
　例えば，高血圧の治療薬で，旧薬による血圧降下の平均値と分散が Mo，σ² であるとき，新薬による血圧降下の平均値が Mn であるとき有効としよう。α = 0.05，β = 0.20 で片側検定を行うときの標本の大きさ n の見積もり（ 各群それぞれの標本の大きさ ）は，δ = Mn - Moとして，次式で求めることができる。

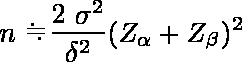
　この式で，Zα，Zβ は標準正規分布のパーセント点である。 Zα = Z0.05 = 1.6449
Zβ = Z0.20 = 0.8416　など
　両側検定の場合の n の見積もりは，上の式で Zα / 2 とすればよい。
　ただ，この方法は正確ではない。正確に計算するためには非心 t 分布を使わなくてはならない。