二群の比率の差の検定
例題:
「内閣の支持率調査で,男の有権者の 300 人中 145 人,女の有権者 250 人中 157 人が支持していた。男女で支持率に差があるかどうか検定しなさい。」
R による解析:
> prop.test(c(145, 157), c(300,250), correct=F) # 連続性の補正をしない場合 2-sample test for equality of proportions without continuity correction data: c(145, 157) out of c(300, 250) X-squared = 11.5266, df = 1, p-value = 0.000686 alternative hypothesis: two.sided 95 percent confidence interval: -0.22705213 -0.06228121 sample estimates: prop 1 prop 2 0.4833333 0.6280000 > prop.test(c(145, 157), c(300,250)) # 連続性の補正をする場合 2-sample test for equality of proportions with continuity correction data: c(145, 157) out of c(300, 250) X-squared = 10.9497, df = 1, p-value = 0.0009362 alternative hypothesis: two.sided 95 percent confidence interval: -0.23071879 -0.05861454 sample estimates: prop 1 prop 2 0.4833333 0.6280000
二群の比率の差の検定
例題:
「内閣の支持率調査で,男の有権者の 300 人中 145 人,女の有権者 250 人中 157 人が支持していた。男女で支持率に差があるかどうか検定しなさい。」
注意:以下に述べるのは,正規分布を用いる近似的な検定方法である。「近似法」という意味は,「サンプルサイズが大きい場合には」という意味合いである。どの程度のサンプルサイズなら近似が成り立つのか心配ならば,サンプルサイズの大きさに関わりなくいつも正確な検定結果を与えるフィッシャーの正確検定を適用することを勧める。
検定手順:
- 記号の定義
第 1 群のケース数を n1,ある特性を持つものの数(陽性数と呼ぶことにする)を r1,第 2 群のケース数を n2,陽性数を r2 とする。
各群の比率を p1 = r1 / n1,p2 = r2 / n2 とする。
例題では,n1 = 300,r1 = 145,n2 = 250,r2 = 157 であるから,p1 = 0.483,p2 = 0.628 となる。
- 前提
- 2 群をプールした全標本中の陽性数の比率 p を,p = (r1+r2) / (n1+n2) としたとき,検定統計量は次式で計算される。
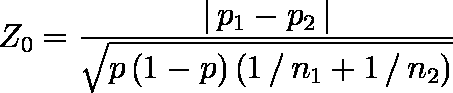
なお,連続性の補正は次式で行われる。
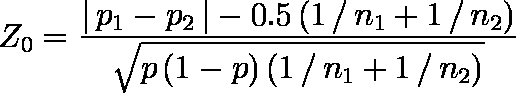
ただし,| p1 - p2 | ≦ 0.5 (1 / n1+1 / n2) のときは,Z0 = 0 とする。
例題では,p = (145+157) / (300+250) = 0.549 であり,Z0 = 3.403 となる(連続性の補正を行った場合は,Z0 = 3.317)。
- Z0 は,正規分布に従う。有意確率を P = Pr{|Z|≧ Z0} とする。
正規分布表,または正規分布の上側確率の計算を参照すること。
例題では,Pr{|Z|≧ 1.96}= 0.05 なので,P = Pr{Z ≧ 3.403}< 0.05 である(正確な有意確率:P = 0.000666502)。
- 帰無仮説の採否を決める。
例題では,有意水準 5% で検定を行うとすれば(α = 0.05),P < α であるから,帰無仮説を棄却する。すなわち,「男女で支持率に差がある」といえる。
二群の比率の差の検定と同じ種類の言葉
- 二群の比率の差の検定のページへのリンク
