独立性の検定とは何？わかりやすく解説 Weblio辞書

独立性の検定

表 1．疾患別の血液型の分布（架空例）
血液型	胃潰瘍患者	胃癌患者	健康者	合計
A 型	16	12	36	64
B 型	12	5	20	37
O 型	15	11	24	50
AB 型	9	2	1	12
合計	52	30	81	163

R による解析：

> tbl5 <- matrix(c(
+ 	16, 12, 36,
+ 	12, 5, 20,
+ 	15, 11, 24,
+ 	9, 2, 1
+ 	), ncol=3, byrow=T)

> tbl5
     [,1] [,2] [,3]
[1,]   16   12   36
[2,]   12    5   20
[3,]   15   11   24
[4,]    9    2    1

> chisq.test(tbl5)

	Pearson's Chi-squared test

data:  tbl5 
X-squared = 13.7134, df = 6, p-value = 0.03301

Warning message: 
Chi-squared approximation may be incorrect in: chisq.test(tbl5)

独立性の検定

例題：
　「13 人の学生について，自動車運転免許を持っているかどうかを調査した結果が，表 4 のようにまとめられた。男女で免許保有率に差があるかどうか検定しなさい。」

表 4．性別の運転免許保有状況（その 1）
	あり	なし	合計
男子	4	2	6
女子	1	6	7
合計	5	8	13

R による解析：

> tbl4 <- matrix(c(4, 2, 1, 6), ncol=2, byrow=T)

> tbl4
     [,1] [,2]
[1,]    4    2
[2,]    1    6

> chisq.test(tbl4, correct=F) # 連続性の補正をしない場合

	Pearson's Chi-squared test

data:  tbl4 
X-squared = 3.7452, df = 1, p-value = 0.05296

Warning message: 
Chi-squared approximation may be incorrect in: chisq.test(tbl4, correct = F) 

> chisq.test(tbl4) # 連続性の補正をする場合

	Pearson's Chi-squared test with Yates' continuity correction

data:  tbl4 
X-squared = 1.8591, df = 1, p-value = 0.1727

Warning message: 
Chi-squared approximation may be incorrect in: chisq.test(tbl4)

注意
4 つの桝目の数値を a，b，c，d，および，n = a + b + c + d としたとき，abs(a * d - b * c) - n / 2 が負の値になるときに，R の chisq.test は誤った答えを表示してしまう。
abs(a*d-b*c)-n/2 が負の値になるときには，補正カイ二乗値は無条件に 0 にしなければならない（手法の解説ページを参照のこと）。

表 5．問題の生じる分割表の例
	あり	なし	合計
男子	10	15	25
女子	11	16	27
合計	21	31	52

R での計算結果

> tbl5 <- matrix(c(10, 15, 11, 16), ncol=2, byrow=TRUE)
> tbl5
     [,1] [,2]
[1,]   10   15
[2,]   11   16
> chisq.test(tbl5)

	Pearson's Chi-squared test with Yates' continuity correction

data:  tbl5 
X-squared = 0.0522, df = 1, p-value = 0.8193

この結果は，間違いである。
abs(10*16-15*11)-52/2 = -21 である。これは，修正される前の数値より，修正すべき数値が大きいという例外が生じているのである。意味的に考えれば，このようなときには修正後の値は 0 とすべきである。そのようにすればカイ二乗値は 0 になり，P 値は 1 になるのである。
対処法は R の chisq.test 関数の中の

            if (correct && nrow(x) == 2 && ncol(x) == 2) {
                YATES <- 0.5
                METHOD <- paste(METHOD, "with Yates' continuity correction")
            }
            else YATES <- 0
            STATISTIC <- sum((abs(x - E) - YATES)^2/E)

という部分を

            if (correct && nrow(x) == 2 && ncol(x) == 2) {
                STATISTIC <- if (abs(x[1,1]*x[2,2]-x[1,2]*x[2,1]) < sum(x)/2) 0 else sum((abs(x - E) - 0.5)^2/E)
                METHOD <- paste(METHOD, "with Yates' continuity correction")
            }
            else STATISTIC <- sum((abs(x - E))^2/E)

のように変更すればよい。

独立性の検定

例題：
　「130 人の学生について，自動車運転免許を持っているかどうかを調査した結果が，表 5 のようにまとめられた。男女で免許保有率に差があるかどうか検定しなさい。」

表 5．性別の運転免許保有状況（その 2）
	あり	なし	合計
男子	40	20	60
女子	10	60	70
合計	50	80	130

R による解析：

> tbl6 <- matrix(c(40, 20, 10, 60), ncol=2, byrow=T)

> tbl6
     [,1] [,2]
[1,]   40   20
[2,]   10   60

> chisq.test(tbl6, correct=F) # 連続性の補正をしない場合

	Pearson's Chi-squared test

data:  tbl6 
X-squared = 37.4524, df = 1, p-value = 9.367e-10

> chisq.test(tbl6) # 連続性の補正をする場合

	Pearson's Chi-squared test with Yates' continuity correction

data:  tbl6 
X-squared = 35.272, df = 1, p-value = 2.867e-09

独立性の検定

例題：
　以下のデータについて，「二群の比率の差の検定」を用いて解きなさい。　「学生について，自動車運転免許を持っているかどうかを調査した結果が，表 4，5 のようにまとめられた。男女で免許保有率に差があるかどうか検定しなさい。」

表 4．性別の運転免許保有状況（その 1）
	あり	なし	合計
男子	4	2	6
女子	1	6	7
合計	5	8	13

表 5．性別の運転免許保有状況（その 2）
	あり	なし	合計
男子	40	20	60
女子	10	60	70
合計	50	80	130

R による解析：

> prop.test(c(4,1), c(6, 7), correct=F) # 連続性の補正をしない場合

	2-sample test for equality of proportions without continuity
	correction

data:  c(4, 1) out of c(6, 7) 
X-squared = 3.7452, df = 1, p-value = 0.05296
alternative hypothesis: two.sided 
95 percent confidence interval:
 0.06612646 0.98149258 
sample estimates:
   prop 1    prop 2 
0.6666667 0.1428571 

Warning message: 
Chi-squared approximation may be incorrect in: prop.test(c(4, 1), c(6, 7), correct = F) 

> prop.test(c(4,1), c(6, 7)) # 連続性の補正をする場合

	2-sample test for equality of proportions with continuity
	correction

data:  c(4, 1) out of c(6, 7) 
X-squared = 1.8591, df = 1, p-value = 0.1727
alternative hypothesis: two.sided 
95 percent confidence interval:
 -0.08863544  1.00000000 
sample estimates:
   prop 1    prop 2 
0.6666667 0.1428571 

Warning message: 
Chi-squared approximation may be incorrect in: prop.test(c(4, 1), c(6, 7)) 

> prop.test(c(40,10), c(60, 70), correct=F) # 連続性の補正をしない場合

	2-sample test for equality of proportions without continuity
	correction

data:  c(40, 10) out of c(60, 70) 
X-squared = 37.4524, df = 1, p-value = 9.367e-10
alternative hypothesis: two.sided 
95 percent confidence interval:
 0.3790774 0.6685416 
sample estimates:
   prop 1    prop 2 
0.6666667 0.1428571 

> prop.test(c(40,10), c(60, 70)) # 連続性の補正をする場合

	2-sample test for equality of proportions with continuity
	correction

data:  c(40, 10) out of c(60, 70) 
X-squared = 35.272, df = 1, p-value = 2.867e-09
alternative hypothesis: two.sided 
95 percent confidence interval:
 0.3636012 0.6840178 
sample estimates:
   prop 1    prop 2 
0.6666667 0.1428571

独立性の検定

　2 変数 A，B についてのクロス集計表（分割表）に基づき，2 変数間に関連があるかどうかを検定する。
　χ² 分布を用いるので，「χ² 検定」という通称を持つ。

例題：
　「表 1 において，血液型と疾患に関連があるかどうか検定しなさい。」

表 1．疾患別の血液型の分布（架空例）
血液型	胃潰瘍患者	胃癌患者	健康者	合計
A 型	16	12	36	64
B 型	12	5	20	37
O 型	15	11	24	50
AB 型	9	2	1	12
合計	52	30	81	163

検定手順：

前提
- 帰無仮説 H0：「2 変数は独立である（関連がない）」。
- 対立仮説 H1：「2 変数は独立ではない（関連がある）」。
- 有意水準 α で両側検定を行う（k × m 分割表では必ず両側検定である。片側検定は理論上あり得ない。ただし，2 × 2 分割表では関連の方向性を決められるので，片側検定もあり得る）。

2 個の変数 A，B がそれぞれ k 個，m 個のカテゴリーを持ち，k × m 個の桝目を持つ集計表を考える（表 2, 3）。
例題では，k = 4，m = 3 である。

表 2．k × m 分割表
		B1	B2	...	Bj	...	Bm	合計
		要因 B
要因 A	A1				O1j			n1・
	A2				O2j			n2・
	：				：			：
	Ai	Oi1	Oi2	...	Oij	...	Oim	ni・
	：				：			：
	Ak				Okj			nk・
	合計	n・1	n・2	...	n・j	...	n・m	n

表 3．2 × 2 分割表
		B1	B2	合計
		要因 B
要因 A	A1	a	b	e
要因 A	A2	c	d	f
	合計	g	h	n

表 2 のような k × m 分割表で，変数 A の第 i カテゴリー，変数 B の第 j カテゴリーの観察値を Oij とする。
また，ni・を第 i 行の合計，n・j を第 j 列の合計とする。
帰無仮説のもとでは，変数 A の第 i カテゴリー，変数 B の第 j カテゴリーの期待値は次式で表される。

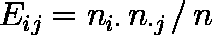
例題では，O 型の胃癌患者の期待値は，E32 = 50・30 / 163 = 9.202 等のように計算される。
全ての桝目について ( Oij - Eij ) ² / Eij の合計をとったものを χ²0 とする。

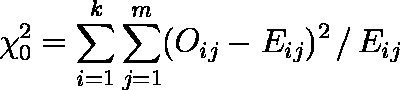
例題では，χ²0 ≒ 13.713 となる。
χ²0 は自由度が（ k - 1 ）×（ m - 1 ）の χ² 分布に従う。
例題では，自由度は ( 4 - 1 ) ×( 3 - 1 ) = 6 である。
有意確率を P= Pr｛ χ² ≧ χ²0 ｝とする。
χ² 分布表，または χ² 分布の上側確率の計算を参照すること。
例題では，自由度 6 の χ² 分布において，Pr｛χ² ≧ 12.59｝= 0.05 であるから，P = Pr｛χ² ≧ 13.713｝＜ 0.05 である（正確な有意確率：P = 0.03301）。
帰無仮説の採否を決める。
- P ＞ α のとき，帰無仮説を採択する。「2 変数は独立でないとはいえない（関連があるとはいえない）」。
- P ≦ α のとき，帰無仮説を棄却する。「2 変数は独立ではない（関連がある）」。
例題では，有意水準 5% で検定を行うとすれば（α = 0.05），P ＜ α であるから，帰無仮説を棄却する。すなわち，「血液型と疾患の間に関連がある」といえる（架空例であったことを思い出してくださいね）。

2 × 2 分割表における特別な方法

簡便公式：表 3 のような 2 × 2 分割表における独立性の検定は，次式を用いることにより若干簡単になる。
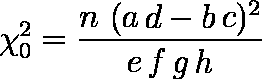
連続性の補正（イエーツの補正）：分割表から得られる χ²0 は跳び跳びの値しかとらない。一方，χ² 分布は連続分布である。このため，2 × 2 分割表の場合には連続性の補正をしたほうがよい。

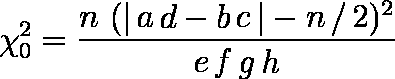
ただし，| a d - b c | ≦ n / 2 のときは，χ²0 = 0 とする。

いくつかの注意点

ウィキペディア小見出し辞書

索引トップ用語の索引ランキング

独立性の検定

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2022/06/17 19:38 UTC 版)

「独立 (確率論)」の記事における「独立性の検定」の解説

「カイ二乗検定」および「分割表」も参照独立性を判断するには、独立性を仮定した上で対象の振る舞いを調べ、独立性を仮定したことによる矛盾が引き出せるかどうかを確認する必要がある。独立性（あるいは従属性）を判別する手段として分割表を用いた独立性の検定がある。独立性の検定に用いられる手法には例えばカイ二乗検定などがある。独立性の検定によって2つの事象の間の従属性を判断することができるが、独立であるかどうか積極的に決定することは難しい。

※この「独立性の検定」の解説は、「独立 (確率論)」の解説の一部です。
「独立性の検定」を含む「独立 (確率論)」の記事については、「独立 (確率論)」の概要を参照ください。

ウィキペディア小見出し辞書の「独立性の検定」の項目はプログラムで機械的に意味や本文を生成しているため、不適切な項目が含まれていることもあります。ご了承くださいませ。お問い合わせ。

独立性の検定と同じ種類の言葉

>>同じ種類の言葉 >>統計に関連する言葉

>> 「独立性の検定」を含む用語の索引
独立性の検定のページへのリンク

独立性の検定とは？わかりやすく解説

独立性の検定

独立性の検定

独立性の検定

独立性の検定

独立性の検定

独立性の検定

「独立性の検定」の関連用語


	Copyright (C) 2024 統計学用語辞典 All rights reserved.
	Text is available under GNU Free Documentation License (GFDL). Weblio辞書に掲載されている「ウィキペディア小見出し辞書」の記事は、Wikipediaの独立 (確率論) (改訂履歴)の記事を複製、再配布したものにあたり、GNU Free Documentation Licenseというライセンスの下で提供されています。

独立性の検定とは？ わかりやすく解説

独立性の検定

独立性の検定

独立性の検定

独立性の検定

独立性の検定

独立性の検定

「独立性の検定」の関連用語

独立性の検定とは？わかりやすく解説