分布の差の検定とは何？わかりやすく解説 Weblio辞書

索引トップ用語の索引ランキング

分布の差の検定

例題：
　「ABO 式の血液型を調べたところ，表 1 のような結果であった。男女で血液型の分布がことなるだろうか。」

表 1．男女の血液型
性別	A	B	O	AB	合計
男	20	15	16	4	55
女	15	7	9	4	35
合計	35	22	25	8	90

R による解析：

> tbl <- matrix(c(
+ 	20, 15, 16, 4,
+ 	15, 7, 9, 4
+ 	), ncol=4, byrow=T)
 
> chisq.test(tbl)

	Pearson's Chi-squared test

data:  tbl 
X-squared = 1.1981, df = 3, p-value = 0.7535

Warning message: 
Chi-squared approximation may be incorrect in: chisq.test(tbl) 

> tbl
     [,1] [,2] [,3] [,4]
[1,]   20   15   16    4
[2,]   15    7    9    4

分布の差の検定

例題：
　「調査対象者の年齢分布を男女ごとに集計すると表 3 のようになった。対象者の年齢構成が同じであるとみなしてよいか，検定しなさい。」

表 3．調査対象者の性別年齢分布
性別	20 歳代	30 歳代	40 歳代	50 歳代	60 歳代	合計
男	11	24	35	43	27	140
女	16	30	46	53	17	162
合計	27	54	81	96	44	302

R による解析：

> tbl2 <- matrix(c(
+ 	11, 24, 35, 43, 27,
+ 	16, 30, 46, 53, 17
+ 	), ncol=5, byrow=T)
> chisq.test(tbl2)

	Pearson's Chi-squared test

data:  tbl2 
X-squared = 4.8238, df = 4, p-value = 0.3059

> tbl2
     [,1] [,2] [,3] [,4] [,5]
[1,]   11   24   35   43   27
[2,]   16   30   46   53   17

分布の差の検定

　クロス集計表（分割表）の形式でまとめられた結果に基づき，複数の群の分布に差があるかどうかを検定する。
　注：実質的には，「独立性の検定」と同じものである。

例題：
　「ABO 式の血液型を調べたところ，表 1 のような結果であった。男女で血液型の分布がことなるだろうか。」

表 1．男女の血液型
性別	A	B	O	AB	合計
男	20	15	16	4	55
女	15	7	9	4	35
合計	35	22	25	8	90

検定手順：

前提
- 帰無仮説 H0：「各群の分布は同じである」。
- 対立仮説 H1：「各群の分布は異なる」。
- 有意水準 α で両側検定を行う（片側検定は定義できない）。

m 個のカテゴリーを持つ観察値が k 群について調べられ，表 2 のようにまとめられているとする。
例題では，m = 4，k = 2 である。

表 2．記号の定義
群	第 1 カテゴリー	第 2 カテゴリー	...	第 m カテゴリー	合計
第 1 群	O11	O12	...	O1m	n1
第 2 群	O21	O22	...	O2m	n2
:	:	:	:	:	:
第 k 群	Ok1	Ok2	...	Okm	nk
合計	t1	t2	...	tm	n

全体としてみたとき，ある個体が第 j カテゴリーに属する確率は tj / n である。
例題では，たとえば A 型である確率は 35/90 ≒ 0.389 である。
第 i 群の第 j カテゴリーの期待値は Eij = ni × (tj / n) である。
例題では，A 型の男に対する期待値は 55 × (35/90) ≒ 21.389 である。
全ての桝目における，期待値からの変位の合計量（検定統計量）を，以下の式で計算する。

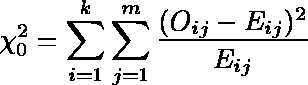
例題では，χ²0 ≒ 1.1981 となる。
χ²0 は，自由度が (k-1) × (m-1) の χ² 分布に従う。
例題では，(2-1) × (4-1) = 3 である。
有意確率を P = Pr｛χ² ≧ χ²0｝とする。
χ²分布表，またはχ²分布の上側確率の計算を参照すること。
例題では，自由度 3 の χ² 分布において，Pr｛χ² ≧ 7.81｝= 0.05 であるから，P = Pr｛χ² ≧ 1.1981 ｝＞ 0.05 である（正確な有意確率：P = 0.75346）。
帰無仮説の採否を決める。
- P ＞ α のとき，帰無仮説を採択する。「各群の分布が同じでないとはいえない」。
- P ≦ α のとき，帰無仮説を棄却する。「各群の分布は同じではない」。
例題では，有意水準 5% で検定を行うとすれば（α = 0.05），P ＞ α であるから，帰無仮説を採択する。すなわち，「男女で血液型の分布は同じでないとはいえない」。