分散の均一性の検定

統計学用語辞典

分散の均一性の検定（バートレットの方法）

例題：
　「12 匹のラットに 3 種類の餌を与えたときの肝臓の重量は表 1 のようであった。餌の種類により肝臓の重量の分散に差があるといえいるか，有意水準 5% で検定しなさい。」

表 1．餌の種類による肝臓の重量

A餌	3.42	3.84	3.96	3.76
B餌	3.17	3.63	3.47	3.44	3.39
C餌	3.64	3.72	3.91

R による解析:

> x <- c(3.42, 3.84, 3.96, 3.76,  3.17, 3.63, 3.47, 3.44, 3.39,  3.64, 3.72, 3.91)
> g <- rep(1:3, c(4, 5, 3)) # 右と同じ　c(rep(1, 4), rep(2, 5), rep(3, 3))
> bartlett.test(x, g)

	Bartlett test for homogeneity of variances

data:  x and g 
Bartlett's K-squared = 0.6182, df = 2, p-value = 0.7341

> x
 [1] 3.42 3.84 3.96 3.76 3.17 3.63 3.47 3.44 3.39 3.64 3.72 3.91
> g
 [1] 1 1 1 1 2 2 2 2 2 3 3 3

分散の均一性の検定（バートレットの方法）

例題：
　「都道府県を 4 つに分けてそれぞれの群における癌による死亡率（人口 10 万人あたり）の集計結果は表 2 のようであった。分散に差があるといえいるか，有意水準 5% で検定しなさい。」

表 2．47 都道府県における癌死亡率

	都道府県数	平均値	標準偏差
第1群	8	135.83	19.59
第2群	11	160.49	12.28
第3群	22	178.35	15.01
第4群	6	188.06	9.81
全体	47	168.17	22.40

R による解析:

> n <- c(8, 11, 22, 6)	# 各群の標本の大きさ
> SD <- c(19.59, 12.28, 15.01, 9.81)	# 各群の標準偏差

> U <- SD^2	# 標準偏差を二乗して，不偏分散を求める
> my.bartlett.test(n, U) # この関数の定義を見る
  Chi sq.      d.f.   P value 
3.1122831 3.0000000 0.3746352 

分散の均一性の検定（バートレットの方法）

例題：
　「12 匹のラットに 3 種類の餌を与えたときの肝臓の重量は表 1 のようであった。餌の種類により肝臓の重量の分散に差があるといえいるか，有意水準 5% で検定しなさい。」

表 1．餌の種類による肝臓の重量

A餌	3.42	3.84	3.96	3.76
B餌	3.17	3.63	3.47	3.44	3.39
C餌	3.64	3.72	3.91

検定手順:

1. 前提
   • 帰無仮説 H0：「各群の母分散は等しい（一様である）　σ²1=σ²2=…σ²k」。
   • 対立仮説 H1：「各群の母分散は等しくない（一様でない）　（σ²1=σ²2=…σ²k）ではない」。
   • 有意水準 α で両側検定を行う（片側検定は定義できない）。
   • データが正規分布に従い，分散は互いに独立であるという二つの条件を満たす必要がある。
   
   
2. 群の数を k，各群の不偏分散を Uj，ケース数を nj とする（j = 1， 2， ... ， k；Σ nj = n）。
   
3. 以下の式で検定統計量 χ²0 を計算する（式中の ln は自然対数である）。
   
   
   
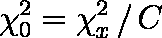
   例題の場合，以下のような補助計算表を作ると計算が楽である。
   

   i	ni	Ui	ni-1	(ni-1)Ui	ln(Ui)	(ni-1) ln(Ui)	1/(ni-1)
   群1	4	0.0537	3	0.1611	-2.9243	-8.7730	0.3333
   群2	5	0.0276	4	0.1104	-3.5899	-14.3598	0.2500
   群3	3	0.0192	2	0.0385	-3.9511	-7.9022	0.5000
   合計	12		9	0.3100	-10.4654	-31.0350	1.0833

   
   χ²x = 0.7184，C = 1.1620 より，χ²0 = 0.6182 となる。
   
4. 検定統計量 χ²0 は，自由度が k - 1 の χ² 分布に従う。
   例題の場合，自由度は 2 である。
   
5. 
   有意確率を P = Pr｛χ² ≧ χ²0｝ とする。
   χ²分布表，または χ² 分布の上側確率の計算を参照すること。
   例題では，自由度 2 の χ² 分布において，Pr｛χ² ≧ 5.99｝= 0.05 であるから，P = Pr｛χ² ≧ 0.6182｝＞ 0.05 である（正確な有意確率：P = 0.7341）。
   
6. 帰無仮説の採否を決める。
   
   • P ＞ α のとき，帰無仮説を採択する。「各群の母分散は等しくないとはいえない」。
   • P ≦ α のとき，帰無仮説を棄却する。「各群の母分散は等しくない」。
   
   例題では，有意水準 5% で検定を行うとすれば（α = 0.05），P ＞ α であるから，帰無仮説を採択する。すなわち，「各群の母分散は等しくないとはいえない」といえる。