せいき‐ぶんぷ【正規分布】
正規分布
正規分布
 標準正規分布表
標準正規分布表  上側確率の計算
上側確率の計算  パーセント点の計算
パーセント点の計算
Excel には,標準正規分布についてnormsdist,normsinv,正規分布についてnormdist,norminvという関数が用意されている。
二つのパラメータ,母平均 μ,母分散 σ2 を持つ正規分布は,N ( μ, σ2 ) と表記される。
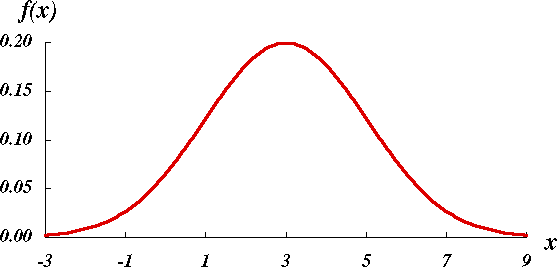 図 1.正規分布 N ( 3, 22 ) の概形 |
|---|
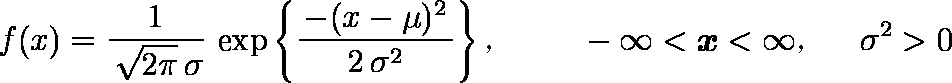
平均 E ( x ) ,分散 V ( x ) は
E ( x ) = μ, V ( x ) = σ2
である。
変数変換z = ( x- μ ) / σ をほどこしたとき(この変数変換のことを 標準化 と呼ぶ),確率変数 zは,平均値 0,分散 1 の正規分布に従い,N ( 0, 12 ) と表される。これを特に,標準正規分布 と呼ぶ。
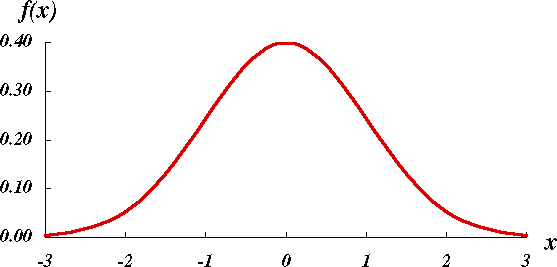 図 2.標準正規分布 N ( 0, 12 ) の概形 |
|---|
図 1 と図 2 を比較するとわかるように,どのような正規分布でも全て相似である。
三角分布では一様分布する 2 つの確率変数を加えたが,n 個の確率変数の和を考え,n を大きくしてゆくと次第に正規分布に近づく( 中心極限定理 の項を参照 )。例えば,12 個の一様乱数を加えたものは,平均値 6,分散 1 の正規分布に従う。
ポアソン分布,二項分布などは極限的な場合に正規分布に近づく。
正規分布についてもう少し詳しく...
正規分布
正規分布
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/04/09 15:30 UTC 版)

|
この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 (2016年4月)
|
| 母数 | 
また、多変量の統計として共分散まで込めた多次元の正規分布も定義され、平均 μ = (μ1, μ2, …, μn) の n 次元正規分布の同時密度関数は次の式で与えられる。
|
出典は列挙するだけでなく、脚注などを用いてどの記述の情報源であるかを明記してください。
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
- ハラルド・クラメール (1946). Mathematical Methods of Statistics. Princeton Mathematical Series. 9. Princeton University Press. MR 0016588. Zbl 0063.01014 (Review by W. Feller)
- 稲垣宣生『数理統計学』裳華房、1990年。 ISBN 4-7853-1406-0。
- JIS Z 8101-1:2015 統計 − 用語と記号 − 第1部:確率及び一般統計用語, 日本規格協会
- Stigler, Stephen M. (1986). The History of Statistics: The Measurement of Uncertainty before 1900. The Belknap Press of Harvard University Press. ISBN 0-674-40340-1. MR 0852410. Zbl 0656.62005
- 日本数学会 編『岩波 数学辞典』(第4版)岩波書店、2007年。 ISBN 978-4-00-080309-0。
- 成実清松、坂井忠次『数理統計学要説』培風館、1952年。doi:10.11501/1371195。NDLJP:1371195。
関連項目
外部リンク
- 正規分布表 (PDF) —— 脇本和昌『身近なデータによる統計解析入門』森北出版、1973年。 ISBN 4627090307。 付表
- 『正規分布』 - コトバンク
正規分布
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/11/09 06:39 UTC 版)
「モーメント (確率論)」の記事における「正規分布」の解説
確率密度関数が p ( x ) = 1 2 π σ exp ( − ( x − μ ) 2 2 σ 2 ) {\displaystyle p(x)={\frac {1}{{\sqrt {2\pi }}\sigma }}\exp \left({-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}\right)} で与えられる正規分布において、n 次の中心モーメントは n が奇数のときは 0 で、偶数のときのみ 0 でない値をとる。 μ n = { 0 ( n : odd ) ( n − 1 ) ! ! σ n ( n : even ) {\displaystyle \mu _{n}={\begin{cases}0&(n:{\text{odd}})\\(n-1)!!~\sigma ^{n}&(n:{\text{even}})\end{cases}}} n!! は二重階乗。
※この「正規分布」の解説は、「モーメント (確率論)」の解説の一部です。
「正規分布」を含む「モーメント (確率論)」の記事については、「モーメント (確率論)」の概要を参照ください。
正規分布
「正規分布」の例文・使い方・用例・文例
正規分布と同じ種類の言葉
- 正規分布のページへのリンク
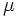 ,
,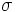 を
を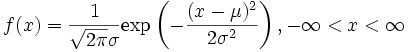
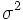 となる. この
となる. この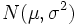 という
という











