スピアマンの順位相関係数
例題:
「表 1 において,変数 X と変数 Y の間のスピアマンの順位相関係数を求めなさい。」
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 変数 Xi | 2.8 | 3.4 | 3.6 | 5.8 | 7.0 | 9.5 | 10.2 | 12.3 | 13.2 | 13.4 |
| 変数 Yi | 0.6 | 3.0 | 0.4 | 1.5 | 15.0 | 13.4 | 7.6 | 19.8 | 18.3 | 18.9 |
計算手順:
- ケース数を n とする。
- 変数 X と変数 Y について,小さい方から順位をつける。同順位がある場合には平均順位をつける。
- 両者の順位の差をとり,di とする(Σ di = 0)。
- Σ di2 は 2 変数の順序の一致性の指標である。
このようなことから,次式を定義すれば, - 1 ≦ rs ≦ 1 となる。これがスピアマンの順位相関係数である。
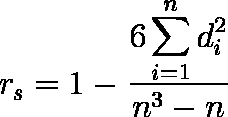
例題では,Σ di2 = 24 であるから,rs = 1 - 6・24 / ( 1000 - 10 ) = 0.85455 となる。
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 変数 Xi の順位 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 変数 Yi の順位 | 2 | 4 | 1 | 3 | 7 | 6 | 5 | 10 | 8 | 9 | |
| 順位の差 di | -1 | -2 | 2 | 1 | -2 | 0 | 2 | -2 | 1 | 1 | Σ di = 0 |
| 順位の差の二乗 di2 | 1 | 4 | 4 | 1 | 4 | 0 | 4 | 4 | 1 | 1 | Σ di2 = 24 |
注:
- どちらか一方(または両方)の変数において全てのケースが同一の値をとる
場合には,スピアマンの順位相関係数は定義できない。
- 同順位がある場合には,変数 X,変数 Y における同順位の個数を nx ,ny ,同順位の大きさを ti ,tj(i = 1,2, ... ,nx;j = 1,2, ... ,ny )としたとき,次式で計算される。同順位がない場合には Tx = Ty = 0 となり,前式に等しくなる。
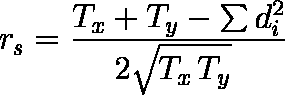
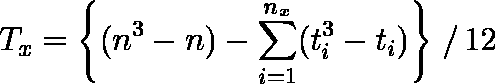
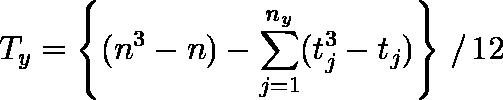
スピアマンの順位相関係数
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/01/04 15:39 UTC 版)

|
この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 (2016年4月)
|

|
この記事は英語版の対応するページを翻訳することにより充実させることができます。(2024年5月)
翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。
|

スピアマンの順位相関係数(スピアマンのじゅんいそうかんけいすう、英: Spearman's rank correlation coefficient)は統計学において順位データから求められる相関の指標である。値は-1以上1以下の実数となり、1ならば単調増加、-1ならば単調減少である。チャールズ・スピアマン(Charles Spearman)によって提唱され[1]、ふつうρ あるいは rS などと書かれる。
ピアソンの積率相関係数(普通に相関係数と呼ばれるもの)と違い、ノンパラメトリックな指標である。すなわち2つの変数の分布について何も仮定せずに、変数の間の関係が任意の単調関数によってどの程度忠実に表現できるかを、評価するものである。「変数間の関係は線形である」と仮定する必要も、また変数を数値的にとる必要もなく、順位が明らかであればよい。
原理的にはスピアマンの順位相関係数はピアソンの積率相関係数の特別な(相関係数を計算する前にデータを順位に変換した)場合に当たる。証明は英語版Wikipediaを参照。しかしρ を計算するには普通もっと単純な手順が用いられる。生のスコアを順位に変換し、各観察(各ペア)における2つの変数の順位の差D を計算する。
定義
スピアマンの順位相関係数 ρ は
- スピアマンの順位相関係数のページへのリンク
