ピアソンの積率相関係数
例題：
「表 1 において，変数 X と変数 Y の間のピアソンの積率相関係数を求めなさい。」
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 変数 Xi | 2.8 | 3.4 | 3.6 | 5.8 | 7.0 | 9.5 | 10.2 | 12.3 | 13.2 | 13.4 |
| 変数 Yi | 0.6 | 3.0 | 0.4 | 1.5 | 15.0 | 13.4 | 7.6 | 19.8 | 18.3 | 18.9 |
計算手順：
- 2 変数 X，Y が n 組あるとする。
- ピアソンの積率相関係数 r は，「変数 X と変数 Y の共分散」と「それぞれの変数の標準偏差」から求められる。
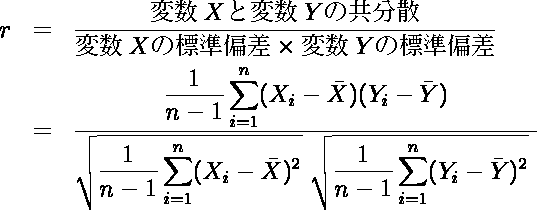
例題では，共分散 Cov.XY = 30.04222222，変数 X の標準偏差 S.D.X = 4.150448436，変数 Y の標準偏差 S.D.Y = 8.082938135 より，r = 0.895504509 となる。
相関係数の大きさと散布図の関係のアニメーション表示，または，ムービー
注：
- どちらか一方（または両方）の変数の分散が 0 のとき（すなわち全てのケースが同一の値をとる場合）には，相関係数は定義できない。
- 相関係数の解釈は表 2 のように行う。母相関係数 = 0 の検定結果と，変数間の相関が実質的に意味があるかどうかは無関係である。
表 2．相関係数の解釈 相関係数の絶対値 解釈 0.0〜0.2 ほとんど相関関係がない 0.2〜0.4 やや相関関係がある 0.4〜0.7 かなり相関関係がある 0.7〜1.0 強い相関関係がある
- いくつかの飛離れた値（＊1）が存在する場合には，それらの値に引きずられて，不当に高い相関係数が得られる。このような場合には順位相関係数を使用したほうがよい。
＊1：このようなデータは測定の誤り，誤記，誤入力等による場合と，実際にそのような値が存在する場合がある。多くの場合，異常値と呼ばれるが，外れ値と呼ぶ方が適切な場合もある。
- 曲線相関の場合には順位相関係数を使用したほうがよい。極端な場合であるが，Y = X2 の関係がある場合に，順位相関係数は 1 になるが，ピアソンの積率相関係数は 1 にはならない。
- 散布図において，観測データが直線的な増減傾向を示しているときには，これらの点の近くを通る直線（回帰直線）を求めることがある（重回帰分析，直線回帰も参照のこと）。
回帰直線の傾き a と切片 b は，次式で求めることができる。
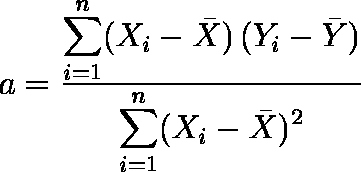
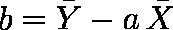
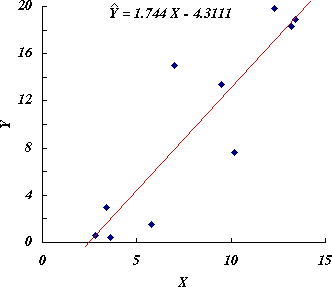
図 1．変数 X を用いて変数 Y を予測する回帰直線
独立変数が X という値をとるとき，予測値
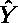の期待値 μ の (1-α)100% 信頼限界は，
自由度が ν= n - 2 の t 分布において，上側確率が α/2 になる値を tα/2,ν，誤差分散を Ve としたとき，以下のように求めることができる。
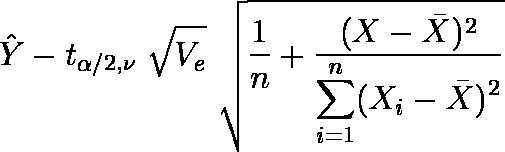…… 下限値
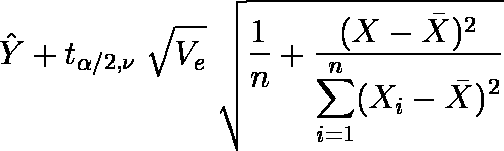…… 上限値ちなみに，Ve は回帰の分散分析において「残差平均平方」のことである。
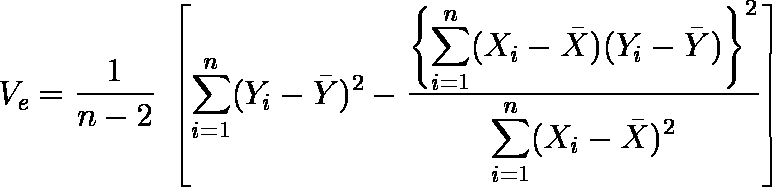
母集団に属する新たな成員 X に対する予測値の信頼区間は，以下のようになる。
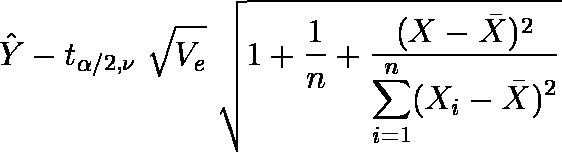…… 下限値
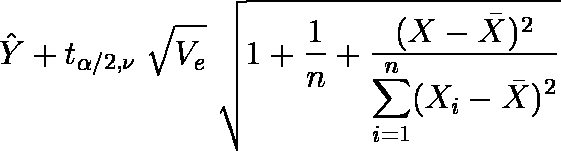…… 上限値
ピアソンの積率相関係数
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2024/11/06 09:49 UTC 版)
ピアソンの積率相関係数（ピアソンのせきりつそうかんけいすう、英: Pearson correlation coefficient, PCC）とは、2つのデータまたは確率変数の間にある線形な関係の強弱を測る指標である[1][2]。カール・ピアソンが研究した。一般的に、単に相関係数といえばピアソンの積率相関係数を指す。
ピアソンの積率相関係数は無次元量で、−1以上1以下の実数に値をとる。相関係数が正のとき確率変数には正の相関が、負のとき確率変数には負の相関があるという。また相関係数が0のとき確率変数は無相関であるという[3][4]。
たとえば、先進諸国の失業率と実質経済成長率は強い負の相関関係にあり、相関係数を求めれば−1に近い数字になる。
相関係数が ±1 に値をとることは、2つのデータ（確率変数）が線形の関係にあるときに限る[5]。また2つの確率変数が互いに独立ならば相関係数は 0 となるが、逆は成り立たない。
定義
母集団相関係数
| 典拠管理データベース: 国立図書館 |
|---|
- ピアソンの積率相関係数のページへのリンク
