ピアソンの積率相関係数の有意性検定
例題:
「標本の大きさが 24,ピアソンの積率相関係数が 0.476 のとき,母相関係数が 0 であるかどうか検定しなさい。」
R による解析:
> cor2.test(24, 0.476) # この関数の定義を見る t d.f. P value 2.5386888 22.0000000 0.0187125
ピアソンの積率相関係数の有意性検定
例題:
「「12 匹の魚について体長と体重の相関係数を求めたところ 0.341 であった。体長と体重に有意な相関関係があるといえるかどうか検定しなさい。」
R による解析:
> cor2.test(12, 0.341) # この関数の定義を見る t d.f. P value 1.1470894 10.0000000 0.2780486
ピアソンの積率相関係数の有意性検定
「母相関係数が 0 以外の特定の値の場合の検定」は,別途用意されている。
例題:
「標本の大きさが 24,ピアソンの積率相関係数が 0.476 のとき,母相関係数が 0 であるかどうか検定しなさい。」
検定手順:
- 前提
- 標本の大きさ(データの組数)を n,標本相関係数を r とする。
例題では,n = 24,r = 0.476 である。
- 次式で検定統計量 t0 を計算する。
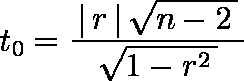
例題では,t0 = 2.53869 となる。
- t0 は,自由度が n - 2 の t 分布に従う。
例題では,自由度は 22 になる。
- 有意確率を P = Pr{|t|≧ t0}とする。
t 分布表,またはt 分布の両側確率の計算を参照すること。
例題では,自由度 22 の t 分布において,Pr{|t|≧ 2.074}= 0.05 であるから,P = Pr{|t|≧ 2.53869}< 0.05 である(正確な有意確率:P = 0.01871)。
- 帰無仮説の採否を決める。
例題では,有意水準 5% で検定を行うとすれば(α = 0.05),P < α であるから,帰無仮説を棄却する。すなわち,「母相関係数は 0 ではない」といえる。
ピアソンの積率相関係数の有意性検定と同じ種類の言葉
| 検定に関連する言葉 | 符号検定 重相関係数の検定 ピアソンの積率相関係数の有意性検定 二標本コルモゴロフスミルノフ検定 シャピロウィルク検定 |
- ピアソンの積率相関係数の有意性検定のページへのリンク
