きたい‐ち【期待値】
期待値
【英】: expected valu
略語: EV
ある試行の結果として、a1 、a2 、……ak になる値が得られる確率がそれぞれ p1 、p2 ……pk である場合、その試行の期待値は E = a1 p1 + a2 p2 +……+ak pk である。E を希望値ということもある。また a1 、a2 、…… ak が収益額などの金額である場合の E を期待額(expected monetary value:EMV)ともいう。期待値は実際に 1 回の試行で必ず起こる値を意味しているわけではない。それは多数回繰り返される試行によって得られる平均値を意味するものである。しかし、期待値は 1 回の試行において起こる可能性が最も高いものとして、不確定要素を含む行為の評価にしばしば用いられる。この概念は石油探鉱計画の評価においても有用である。例えば 500 千ドルの費用を投じて試掘を行う場合に、空井戸になって 500 千ドルの損失となる確率が 80 %、収益 2 百万ドルを得られるような油田が発見される確率が 3 %、収益 5 百万ドルを得られるような油田発見の確率が 10 %、収益 10 百万ドルを得られるような油田発見の確率が 5 %、収益 20 百万ドルが得られるような油田発見の確率が 2 %と思われるならば、期待値は下の計算例のように 1.06 百万ドルとなる。
|
||||||||||||||||||||||
期待値 expectation
期待値
きたいち【期待値】
| 理論上(計算上)、○○を期待できる確率のこと。多くは○○に「大当たり」や「ボーナス」が入る。例えば、「CR新海物語M27の時短中に大当たりを引き戻す期待値は27.2%」というように使われる。 |
期待値
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/02/19 13:26 UTC 版)

|
この記事は英語版の対応するページを翻訳することにより充実させることができます。(2024年5月)
翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。
|
確率論における期待値(きたいち、英: expected value)は確率変数を含む関数の実現値に確率の重みをつけた加重平均である[1]。
期待値
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2019/01/19 05:11 UTC 版)
測定値(各固有値)にその出現確率を掛けて合計した値、つまり測定値の期待値(平均値)は ∑ n P ( a n ) a n = ⟨ ψ | A ^ | ψ ⟩ {\displaystyle \sum _{n}P(a_{n})a_{n}=\langle \psi |{\hat {A}}|\psi \rangle } で表される。これは実数値である。 オブザーバブルを測定するとその観測過程が、非決定論的ではあるが確率的には予測可能な形で状態に変化を与える。すなわち、単一のベクトルで記述されていた状態が、観測により統計的集団へ不可逆的に変化する(現実の測定ではこの集団に含まれるいずれかのベクトルに収縮すると解釈できる)。それゆえオブザーバブルは一般には非可換である。ただし何をもって「観測」と解釈するかは観測問題と呼ばれる一大問題で、現在でも議論が続いている。
※この「期待値」の解説は、「オブザーバブル」の解説の一部です。
「期待値」を含む「オブザーバブル」の記事については、「オブザーバブル」の概要を参照ください。
「期待値」の例文・使い方・用例・文例
期待値と同じ種類の言葉
「期待値」に関係したコラム
GMOクリック証券の提供するバイナリーオプションのハイローの解説
GMOクリック証券株式会社の提供するバイナリーオプションは、外為オプション(外為OP)というサービス名で、ハイロー(HIGH&LOW)を提供しています。2012年5月現在、取り扱っている通貨ペアは、U...
- 期待値のページへのリンク
 の
の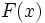 とするとき,
とするとき, 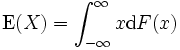 で
で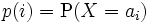 をもつ
をもつ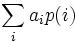 ,
, 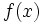 をもつ
をもつ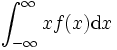 で
で

