辞書ショートカット
カテゴリ一覧
すべての辞書の索引
「離散型分布」の関連用語
| 離散型分布のお隣キーワード |
検索ランキング
離散型分布のページの著作権
Weblio 辞書
情報提供元は
参加元一覧
にて確認できます。
| Copyright (C) 2025 統計学用語辞典 All rights reserved. | |
| Copyright (C) 2025 (社)日本オペレーションズ・リサーチ学会 All rights reserved. |
ビジネス|業界用語|コンピュータ|電車|自動車・バイク|船|工学|建築・不動産|学問
文化|生活|ヘルスケア|趣味|スポーツ|生物|食品|人名|方言|辞書・百科事典
|
ご利用にあたって
|
便利な機能
|
お問合せ・ご要望
|
会社概要
|
ウェブリオのサービス
|
©2025 GRAS Group, Inc.RSS
 が
が 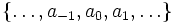
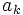 にその値をとる
にその値をとる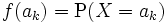 によって
によって )
)
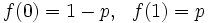
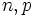 )
)
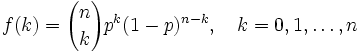
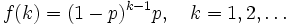
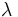 )
)
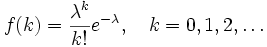
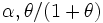 )
)
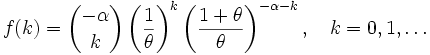
 )
)