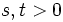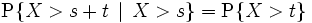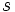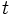無記憶性 (指数分布の)
無記憶性
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/10/24 05:32 UTC 版)
無記憶性(むきおくせい、英語: Memorylessness)とは、確率論や統計学における確率分布の性質の一つ。 直感的な説明としては、無記憶性を持つ確率分布では、過去の失敗や経過時間が将来の試行やさらなる待機時間に影響しない。幾何分布と指数分布のみがこの性質を持つ。
定義
離散的または連続的な確率変数 が無記憶であるとは、任意の非負なる に対して以下の式が成立することを指す:
ここで、 は事象Aが生起する確率、は、事象Bのもとで事象Aが生起する条件付き確率をそれぞれ表す[1][2]。
無記憶性のある確率分布においては、それまでの 回の試行や だけの経過時間のもとでの結果が、その後の 回の試行や だけの経過時間を増やした場合の結果と独立である。すなわち、既存の結果が将来的な観測に関してなんの影響も及ぼさない。
この等式は、離散的な確率変数に対して幾何分布を、また連続的な確率変数に対して指数分布をそれぞれ特徴づける[1][3]。すなわち、幾何分布は無記憶性を持つ唯一の離散確率分布であり、指数分布は無記憶性を持つ唯一の連続確率分布である。
離散確率分布においては、定義式が
と変更されることがある。この場合、 の最小値が (ではなく) である状況を記述する[4][5]。
指数分布の特徴付け
ある連続確率分布が無記憶性を持つ場合、その確率分布は指数分布である。このことは以下のようにして証明できる。
無記憶性の定義式から、以下が成立する:条件付き確率の定義式より、上の式を以下のように変換できる:生存関数を導入すれば、上の式をと書き直せる。この式で を代入することで、任意の自然数 と非負なる実数 に対してが成立することがわかる。
さらに、この式で とおいて両辺を 乗する事で、任意の自然数 と非負なる実数 に対して
が成立することもわかる。これらを組み合わせることで、任意の非負なる有理数 と非負なる実数 に対して
が成立することが示される。有理数の稠密性と生存関数の連続性より、この関係性は任意の非負なる実数に対しても成立する。結果的に、 とおけば、任意の非負実数 に対する生存関数がで与えられるということがわかる。これは指数関数の生存関数に他ならない[3]。
幾何分布の特徴付け
ある離散確率分布が無記憶性を持つ場合、その確率分布は幾何分布である。このことは以下のようにして証明できる。ただし、 の台はであるとする。
連続確率分布と同様の手順により、離散確率分布の場合でもが導かれる。いま、 を1以上の自然数であるとすると、
が得られるので、上の式を繰り返し適用することで、1以上の自然数 に対しが成立していることがわかる。また、 は1以上の整数値を取るので、 ならば である。これらを踏まえると、任意の非負なる実数 に対してが
で表されることがわかる(ただし、 は 以下の整数のうち最大のものを表す)。したがって、この変数の累積分布関数はという形となっている。ここで、とおけば
が得られる。これは幾何分布の累積分布関数に他ならない。
脚注
- ^ a b Dekking, Frederik Michel; Kraaikamp, Cornelis; Lopuhaä, Hendrik Paul; Meester, Ludolf Erwin (2005). A Modern Introduction to Probability and Statistics. Springer Texts in Statistics. London: Springer London. p. 50. doi:10.1007/1-84628-168-7. ISBN 978-1-85233-896-1
- ^ Pitman, Jim (1993) (英語). Probability. New York, NY: Springer New York. p. 279. doi:10.1007/978-1-4612-4374-8. ISBN 978-0-387-94594-1
- ^ a b Riposo, Julien (2023) (英語). Some Fundamentals of Mathematics of Blockchain. Cham: Springer Nature Switzerland. pp. 8–9. doi:10.1007/978-3-031-31323-3. ISBN 978-3-031-31322-6
- ^ Johnson, Norman L.; Kemp, Adrienne W.; Kotz, Samuel (2005-08-19) (英語). Univariate Discrete Distributions. Wiley Series in Probability and Statistics (1 ed.). Wiley. pp. 210. doi:10.1002/0471715816. ISBN 978-0-471-27246-5
- ^ Weisstein. “Memoryless” (英語). mathworld.wolfram.com. 2024年12月2日時点のオリジナルよりアーカイブ。2024年7月25日閲覧。
無記憶性
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2019/01/13 06:16 UTC 版)
幾何分布の重要な性質として、無記憶性と呼ばれるものがある。幾何分布では、いかなる成功確率 p に対しても ∀ n , k ∈ N , P ( X > n + k ∣ X > n ) = P ( X > k ) {\displaystyle \forall n,k\in \mathbb {N} ,\ \ \ P(X>n+k\mid X>n)=P(X>k)} なる等式が成り立つ。これはコイントスを例にすると、コイントスを繰り返して少なくとも n 回表が出なかったという情報が与えられたときに、表が出るまでに投げる回数が n + k を超える条件付き確率は、情報が与えられない場合の確率(すなわち、今すべてを忘れて改めてコイントスを開始して、表が出るまでに投げる回数が k 回を超える確率)に等しいという意味である。 各種のギャンブルにおいて負けが続くと、しばしば「運がたまっている」とか「そろそろ勝ちが巡ってくる」といった考えに陥りがちである。しかし、試行の独立性を仮定する限りにおいては、この考えは誤謬であり、負けが続いているという情報は未来の確率に何の影響も与えないということが、無記憶性からいえる。 この逆、すなわち無記憶性を持つ離散型確率分布が幾何分布のみであることも、比較的容易に示される。
※この「無記憶性」の解説は、「幾何分布」の解説の一部です。
「無記憶性」を含む「幾何分布」の記事については、「幾何分布」の概要を参照ください。
- 無記憶性のページへのリンク
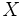 が
が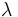 の
の