特性関数 (ゲーム理論の)
【英】:characteristic function
各提携に対し, その提携を形成し, 共同行動をとることによって獲得可能な利得の総和を表す関数である. 数学的にはプレイヤー全体の提携$N$の部分集合の全体から実数への関数である. 利得の総和が意味をもつためには条件(譲渡可能効用, 別払いの存在)が必要となるが,そのような条件が満たされない場合は特性関数値は各プレイヤーの獲得可能な利得ベクトルの集合となる.
特性関数 (確率変数の)
特性関数 (確率論)
(特性関数 から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2024/03/22 00:56 UTC 版)

確率論と統計学において、任意の確率変数に対する特性関数(とくせいかんすう、英: characteristic function)とは、その確率分布を完全に定義する関数である。したがって、確率密度関数や累積分布関数の代わりに特性関数を解析の基盤とすることもできる。確率変数の重み付き総和で分布を定義する単純な特性関数も存在する。
1 変量の分布以外にも、ベクトルまたは行列型の確率変数についての特性関数もあり、さらに一般化することもできる。
実数引数をとる関数と考えたとき、特性関数は積率母関数とは異なり、常に存在する。特性関数の振る舞いとその分布の属性には、モーメントの存在や密度関数の存在などの関係がある。
導入
特性関数
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/03/09 00:53 UTC 版)
レヴィ分布の特性関数は以下の式で与えられる。 φ ( t ; μ , c ) = e i μ t − − 2 i c t . {\displaystyle \varphi (t;\mu ,c)=e^{i\mu t-{\sqrt {-2ict}}}.} この関数は安定分布で使用される形式を用いると以下のように書ける。ただし α = 1/2, β = 1: φ ( t ; μ , c ) = e i μ t − | c t | 1 / 2 ( 1 − i sign ( t ) ) . {\displaystyle \varphi (t;\mu ,c)=e^{i\mu t-|ct|^{1/2}~(1-i~\operatorname {sign} (t))}.}
※この「特性関数」の解説は、「レヴィ分布」の解説の一部です。
「特性関数」を含む「レヴィ分布」の記事については、「レヴィ分布」の概要を参照ください。
- 特性関数のページへのリンク
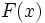 をもつ
をもつ
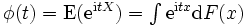 で
で は
は は
は


