積率母関数
ある分布を特徴づけるとき,その積率を計算すれば便利なことがある。積率母関数 は積率を統一的に表現するものとして使用される。
次式のような関数を考える。
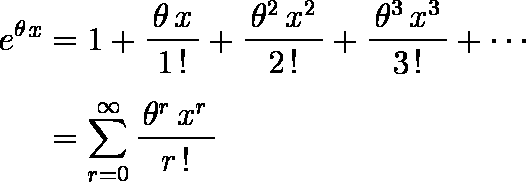
この両辺について期待値を取ってみる。すると,離散型ならば
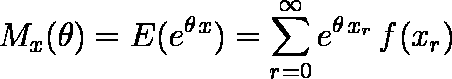
また,連続型ならば,
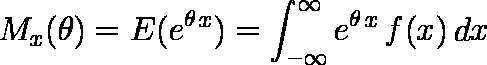 …… (1)
…… (1)となる。この Mx ( θ ) を 積率母関数 という。( 1 )式は,
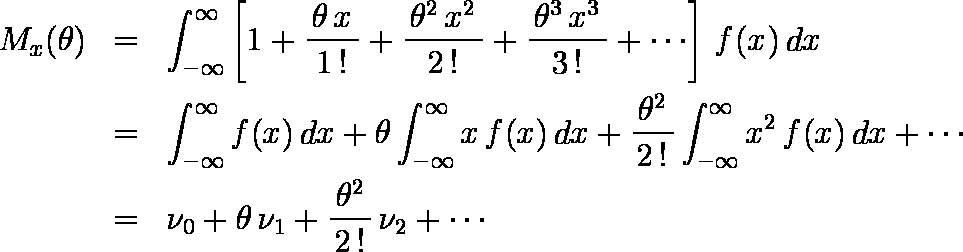
となり,変数の積率母関数が見いだされて,θ のベキ級数に展開することができるならば,xの積率(特にμ,σ2 )は単にその展開式を調べることで直ちに統一的に求めることができる。すなわち,特定の次数,例えば第 r 次の積率を求めたいならば,Mx ( θ ) を r 回微分し,θ = 0 とおいて求めることができる。
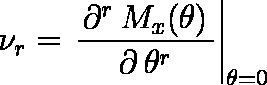
積率母関数
積率母関数
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2020/06/05 19:03 UTC 版)
ナビゲーションに移動 検索に移動

|
この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。
出典を追加して記事の信頼性向上にご協力ください。(2017年2月) |
確率論や統計学において、確率変数 X の積率母関数またはモーメント母関数(英: moment-generating function)は、期待値が存在するならば次の式で定義される。
積率母関数がそのように呼ばれるのは、t = 0 の周囲の開区間上でそれが存在する場合、それが確率分布のモーメントの母関数であるからである。
積率母関数がそのような区間について定義される場合、それにより確率分布が一意に決定される。
積率母関数で重要なことは、積分が収束しない場合、積率(モーメント)と積率母関数が存在しない可能性がある点である。これとは対照的に特性関数は常に存在するため、そちらを代わりに使うこともある。
より一般化すると、n-次元の確率変数ベクトル(ベクトル値確率変数) の場合、 の代わりに を使い、次のように定義する。
計算
積率母関数はリーマン=スティルチェス積分で次のように与えられる。
ここで F は累積分布関数である。
X が連続な確率密度関数 f(X) を持つ場合、 は f(x) の両側ラプラス変換である。
ここで、 は i番目のモーメントである。
2つの独立確率変数の和
2つの独立な確率変数の和の積率母関数は次のようになる。
独立確率変数の総和(一般化)
X1, X2, ..., Xn が一連の独立確率変数で(分布が同一である必要は無い)、
としたとき(ai は定数)、Sn の確率密度関数はそれぞれの Xi の確率密度関数の畳み込みとなり、Sn の積率母関数は次のようになる。
他の関数との関係
積率母関数に関連して、確率論にはいくつかの変換が存在する。
- 特性関数
- 特性関数 と積率母関数は という関係にある。すなわち、特性関数は iX の積率母関数であり、X の積率母関数を虚数軸で評価したものである。
- キュムラント母関数
- キュムラント母関数は積率母関数の対数として定義される。特性関数の対数をキュムラント母関数とする場合もあるが、通常そちらは「第2」キュムラント母関数と呼ぶ。
- 確率母関数
- 確率母関数は で定義される。したがって、 である。
具体例
| 分布 | 積率母関数 |
|---|---|
| 二項分布 | |
| コーシー分布 | 存在しない[1]。 |
| 指数分布 | for |
| 正規分布 | |
| ポアソン分布 |
注
- ^ Allan Gut: Probability: A Graduate Course. Springer-Verlag, 2012, ISBN 978-1-4614-4707-8, Chapter 8, Example 8.2.
積率母関数
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2019/03/30 19:16 UTC 版)
積率母関数は次の通りである。 M x = E ( e t x ) = e t b − e t a t ( b − a ) {\displaystyle M_{x}=E(e^{tx})={\frac {e^{tb}-e^{ta}}{t(b-a)}}} ここから積率 mk を計算することができる。 m 1 = a + b 2 , m 2 = a 2 + a b + b 2 3 , m k = 1 k + 1 ∑ i = 0 k a i b k − i . {\displaystyle {\begin{aligned}m_{1}&={\frac {a+b}{2}},\\m_{2}&={\frac {a^{2}+ab+b^{2}}{3}},\\m_{k}&={\frac {1}{k+1}}\sum _{i=0}^{k}a^{i}b^{k-i}.\\\end{aligned}}} この分布に従う確率変数では、期待値は m1 = a + b/2 となり、分散は m 2 − m 1 2 = ( b − a ) 2 12 {\displaystyle m_{2}-{m_{1}}^{2}={\frac {(b-a)^{2}}{12}}} となる。
※この「積率母関数」の解説は、「連続一様分布」の解説の一部です。
「積率母関数」を含む「連続一様分布」の記事については、「連続一様分布」の概要を参照ください。
- 積率母関数のページへのリンク
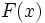 をもつ
をもつ
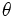 を
を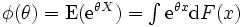 を積率母関数と呼ぶ. 積率母関数が
を積率母関数と呼ぶ. 積率母関数が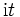 (
(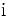 は
は














![G(z) = E[z^X]\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/688e6a2eef74c00803f85123110c2a37b0fcfc84)
![G(e^t) = E[e^{tX}] = M_X(t)\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/55667f3d34d1a4fe9e3a97163142172cbfae5134)










