コーシー分布(コーシーぶんぷ、英語: Cauchy distribution)は、連続確率分布の一種である。分布の名称は、フランスの数学者オーギュスタン=ルイ・コーシーに因む。確率密度関数は以下の式で与えられる。
-
![{\displaystyle f(x;x_{0},\gamma )={\frac {1}{\pi \gamma \left[1+\left({\dfrac {x-x_{0}}{\gamma }}\right)^{2}\right]}}={\frac {1}{\pi }}{\frac {\gamma }{(x-x_{0})^{2}+\gamma ^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdd35eaeb77ca84c013594644b063f649a1ec9cc)
ここで x0 は分布の最頻値を与える位置母数(英語版)、γ は半値半幅を与える尺度母数(英語版)である。
この分布は、ヘンドリック・ローレンツの名を取ってローレンツ分布と呼ばれることもあり、またこれら2人の名前を合わせてコーシー-ローレンツ分布とも呼ばれる。また物理学の分野では、ブライト・ウィグナー分布という名前で知られている。この分布は強制共鳴を記述する微分方程式の解となることから、物理学では重要な存在となっている。また分光学では共鳴広がりを含む多くのメカニズムによって広げられたスペクトル線の形状を記述するために用いられる。以下では、統計学における名称であるコーシー分布を用いて説明する。
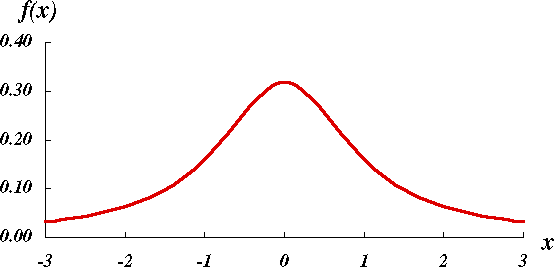
x0 = 0, γ = 1 である場合、この分布は標準コーシー分布と呼ばれ、以下の確率密度関数で与えられる。
-

性質
累積分布関数は以下のようになる。
-

また、逆累積分布関数は次の通りである。
-

コーシー分布は、期待値や分散(およびより高次のモーメント)が定義されない分布の例として知られる。最頻値と中央値は常に定義され、それらはいずれも x0 で与えられる。
X をコーシー分布に従う確率変数とする。コーシー分布の特性関数は以下のように与えられる。
-

U と V を標準正規分布(期待値0、分散1の正規分布)に従う互いに独立な確率変数であるとすると、それらの比 U / V は標準コーシー分布に従う。
X1, X2, …, Xn をあるコーシー分布に従う独立な確率変数列とすると、それらの算術平均
 は再び同じ位置母数、尺度母数を持つコーシー分布に従う(再生性)。この性質は、算術平均の特性関数が
は再び同じ位置母数、尺度母数を持つコーシー分布に従う(再生性)。この性質は、算術平均の特性関数が
-

となることから導かれる。このように、コーシー分布に従う確率変数を増やしても、その算術平均の分布は正規分布に近づかないため、中心極限定理における有限分散の仮定は必須であることが分かる。また、これは安定分布族(コーシー分布は安定分布族に含まれる)における一般化中心極限定理の例でもある。
コーシー分布は無限分解可能な分布である。
自由度1のT分布は、標準コーシー分布と一致する。
コーシー分布が属している位置尺度母数分布族は、実係数メビウス変換に関して閉じている。
特性関数の求め方
コーシー分布の特性関数の求め方は、標準コーシー分布の確率密度関数
-

が複素平面上で x = ±i のみに1位の極を持つことを利用し、留数定理を用いて算出する。
期待値が定義されない理由
コーシー分布の期待値は、
 と置換すると
と置換すると
-
![{\displaystyle {\begin{aligned}\operatorname {E} [x]&=\int _{-\infty }^{\infty }xf(x)\,dx=\int _{-\infty }^{\infty }x_{0}f(x)\,dx+\int _{-\infty }^{\infty }(x-x_{0})f(x)\,dx\\&=x_{0}+{\frac {\gamma }{\pi }}\int _{-\infty }^{\infty }{\frac {x-x_{0}}{(x-x_{0})^{2}+\gamma ^{2}}}\,dx\\&=x_{0}+{\frac {\gamma }{\pi }}\lim _{R_{1},R_{2}\to \infty }\int _{-R_{1}}^{R_{2}}{\frac {z}{1+z^{2}}}\,dz=x_{0}+{\frac {\gamma }{2\pi }}\lim _{R_{1},R_{2}\to \infty }\left[\log(1+z^{2})\right]_{-R_{1}}^{R_{2}}\\&=x_{0}+{\frac {\gamma }{2\pi }}\lim _{R_{1},R_{2}\to \infty }\log \left({\frac {1+{R_{2}}^{2}}{1+{R_{1}}^{2}}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ea9adc9d0fc36876d85856a124c4ea1a09f9747)
となるが、この広義積分の値は存在せず(十分大きな R1, R2 について、
 は
は
 のどのような値でも取りうるので、二重極限としての収束値は存在しない)、このため期待値は存在しない。なお、コーシーの主値
のどのような値でも取りうるので、二重極限としての収束値は存在しない)、このため期待値は存在しない。なお、コーシーの主値
 は x0 である。
は x0 である。
大数の強法則など、期待値に関する確率論のさまざまな結果は、このようなケースでは成立しない。
また、コーシー分布に従う母集団から無作為抽出された標本に関する算術平均は、ただ一つの抽出による結果からは一切改善されない。これは、標本に極端に大きな(あるいは小さな)値が含まれる可能性がかなり高いからである。しかし、標本中央値(これは極端な値には影響を受けない)は中心(最頻値)を知るための一つの尺度となりうる。
2次モーメントが無限大になる理由
期待値が定義されない限り、分散や標準偏差を考えることは不可能である。しかし、原点を中心とした2次モーメントを考えることは可能である。しかし、これもまた無限大となる。
-

相対論的ブライト・ウィグナー分布
原子核物理学および素粒子物理学において、共鳴のエネルギー特性は相対論的ブライト・ウィグナー分布によって記述される。
関連項目
|
|
離散単変量で
有限台 |
|
離散単変量で
無限台 |
|
連続単変量で
有界区間に台を持つ |
|
連続単変量で
半無限区間に台を持つ |
|
連続単変量で
実数直線全体に台を持つ |
|
連続単変量で
タイプの変わる台を持つ |
|
| 混連続-離散単変量 |
|
| 多変量 (結合) |
|
| 方向 |
|
| 退化と特異 |
|
| 族 |
|
| サンプリング法(英語版) |
|
|
|
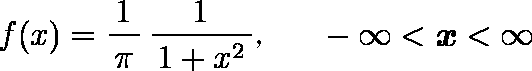










![{\displaystyle f(x;x_{0},\gamma )={\frac {1}{\pi \gamma \left[1+\left({\dfrac {x-x_{0}}{\gamma }}\right)^{2}\right]}}={\frac {1}{\pi }}{\frac {\gamma }{(x-x_{0})^{2}+\gamma ^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fdd35eaeb77ca84c013594644b063f649a1ec9cc)








![{\displaystyle {\begin{aligned}\operatorname {E} [x]&=\int _{-\infty }^{\infty }xf(x)\,dx=\int _{-\infty }^{\infty }x_{0}f(x)\,dx+\int _{-\infty }^{\infty }(x-x_{0})f(x)\,dx\\&=x_{0}+{\frac {\gamma }{\pi }}\int _{-\infty }^{\infty }{\frac {x-x_{0}}{(x-x_{0})^{2}+\gamma ^{2}}}\,dx\\&=x_{0}+{\frac {\gamma }{\pi }}\lim _{R_{1},R_{2}\to \infty }\int _{-R_{1}}^{R_{2}}{\frac {z}{1+z^{2}}}\,dz=x_{0}+{\frac {\gamma }{2\pi }}\lim _{R_{1},R_{2}\to \infty }\left[\log(1+z^{2})\right]_{-R_{1}}^{R_{2}}\\&=x_{0}+{\frac {\gamma }{2\pi }}\lim _{R_{1},R_{2}\to \infty }\log \left({\frac {1+{R_{2}}^{2}}{1+{R_{1}}^{2}}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ea9adc9d0fc36876d85856a124c4ea1a09f9747)




