にこう‐ぶんぷ〔ニカウ‐〕【二項分布】
二項分布
読み方： にこうぶんぷ
【英】: binomial distribution
【英】: binomial distribution
1 回の試行においてある事象が起こる確率が p であるとき、この試行が互いに独立に n 回繰り返される場合に、その事象が i 回起こる確率 P(i) は下式で計算され、その値を i ＝ 0 、1 、2 、……、n について展開した確率分布を二項分布という。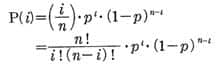 ここに、i! は i の階乗 [i×（i－1）×（i－2）×……×2×1] である。今かりに試掘の成功確率が一定で p ＝ 0.2 と仮定し、また何回もの試掘の結果は互いに影響を与えず独立であるとすると、n 回の試掘をして i 坑が成功する確率は表のとおりである。これによれば、最も確率が高いのは、i ＝ 0.2n の場合であるのは当然であるが、一方、試掘数nが小さいときには全く成功しない（i＝0）確率もかなりあることがわかる 表 二項分布
| |||||||||||||||||||||
二項分布
ある集団において，特性 A を持つものの割合が p であり，持たないものの割合が q であるとする（ p + q = 1 ）。このとき，集団から無作為に n 人を抽出したとき，特性 A を持つものが x 人である確率を考える。n 人のうち x 人が特性を持つ組合せは nCx 通りある（
とも書く） 。その各々に対して，x 人が特性 A を持つ確率は px，残り n - x 人が特性を持たない確率は qn - x であり，両者が共に起こるのは両者の積である。よって，f ( x ) = nCx px qn - x， x = 0,1, … ,n，p ＞ 0，q ＞ 0，p + q = 1 ……(1)
が求める確率であり，この分布を 二項分布 と呼ぶ。
（n，p，q は定数である。このようなパラメータのことを 母数 という。n，p を与えることにより，この分布は確定する。p を 母比率 という。この分布を B ( n, p ) と表すことにする。）。
図 1 は出現率が 0.25 のとき，n = 10 と n = 70 について図示したものである。二項分布では p = q = 0.5 のときに左右対称な密度分布を持つが，p と q がかなり違う場合でも，n が大きくなるにつれ，その形は次第に左右対称なものに近づく（アニメーション，または，ムービー）。
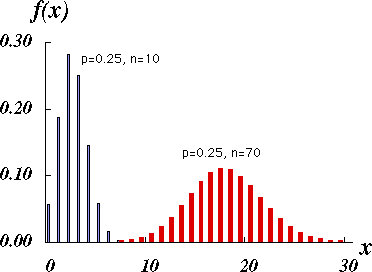 図 1．二項分布の概形 |
|---|
二項分布の平均 E ( x ) と分散 V ( x ) は
E ( x ) = n p， V ( x ) = n p q
である。
ところで，1 回ごとの事象の生起確率 p が一定であるとき，実験を繰り返し行うことを ベルヌーイ試行 というが，独立に実験を n 回繰り返したとき，x 回事象が生じる確率は二項分布である。このため二項分布は ベルヌーイ分布 とも呼ばれる。
問題： 「生まれてくる子どもの性比を，男：女 = 22:21 としたとき，ある団地で 5 人の子どもが生まれるとして，そのうちの 4 人以上が男，あるいは，4 人以上が女である確率を求めよ。」
解答： 求めるのは，（ 1 ）式を用いて，
f ( 0 ) + f ( 1 ) + f ( 4 ) + f ( 5 ) = 1 - ｛ f ( 2 ) + f ( 3 ) ｝ である。
答えは，0.37567586。
二項分布
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2023/12/28 00:58 UTC 版)
| 確率質量関数  | ||
| 累積分布関数  色は上図と同じ | ||
| 母数 |  | この節の内容の信頼性について検証が求められています。 |
|---|---|---|
期待値 np および分散 np(1 − p) が 5 よりも大きい場合、二項分布 B(n, p) に対する良好な近似として正規分布がある。ただし、この近似を適用するにあたっては、変数のスケールに注意し、連続な分布への適切な処理がなされる必要がある。より厳密に述べれば、n が十分大きくかつ、期待値 np および 分散 np(1 − p) も十分大きい場合、期待値 np, 分散 np(1 − p) の正規分布 N(np, np(1 − p)) で近似することができ、期待値からの差 |k − np| が標準偏差 
一覧
カテゴリ
「二項分布」の例文・使い方・用例・文例
二項分布と同じ種類の言葉
- 二項分布のページへのリンク
