![[数式]](https://cdn.weblio.jp/e7/img/dict/tmcyg/img/glossary_scheme_024.gif){kind=small}
が
二項定理
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2025/05/19 22:28 UTC 版)
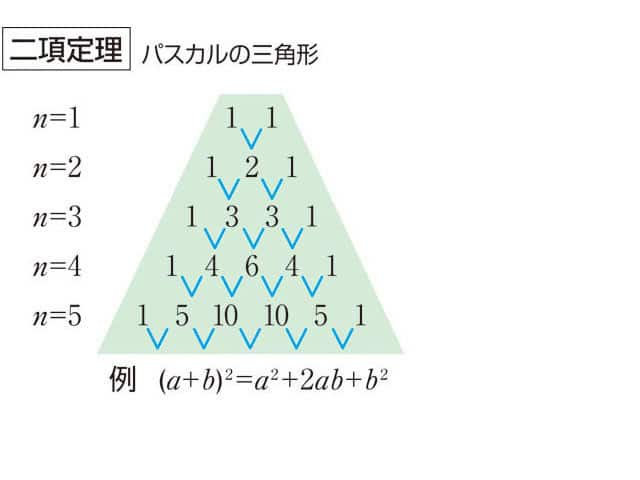
初等代数学における二項定理（にこうていり、英: binomial theorem）または二項展開 (binomial expansion) とは、二項式の冪を代数的に展開した式を表したものである。
定理の主張から、冪 (x + y)n を展開すると、n次の項 (n
k) xn−k yk (0 ≤ k ≤ n)[注 1]の総和になる。ここでの係数 (n
k) を二項係数と呼び、正整数となる。
二項係数 (n
k) は2つの観点から解釈することができる。一つには
- 日本大百科全書(ニッポニカ)『二項定理』 - コトバンク
- 『二項定理の意味と係数を求める例題・２通りの証明』 - 高校数学の美しい物語
- 『一般化二項定理とルートなどの近似』 - 高校数学の美しい物語
- Weisstein, Eric W. "Binomial Theorem". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Binomial Series". mathworld.wolfram.com (英語).
- Weisstein, Eric W. "Negative Binomial Series". mathworld.wolfram.com (英語).
- Solomentsev, E. D. (2001), “Binomial series”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Solomentsev, E.D. (2001), “Newton binomial”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Wolframデモンストレーションプロジェクト
- Binomial Theorem スティーブン・ウルフラム
- Binomial Theorem (Step-by-Step) by Bruce Colletti and Jeff Bryant.
| 典拠管理データベース: 国立図書館 |
|---|
二項定理
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2020/05/26 11:07 UTC 版)
ゴールドシュミット法は、二項定理を使ってより単純化した係数を使うことができる。 D ∈ ( 1 2 , 1 ] {\displaystyle D\in ({\tfrac {1}{2}},1]} となるよう N/D を2の冪でスケーリングすることを前提とする。ここで D = 1 − x {\displaystyle D=1-x} となるよう x を求め、 F i = 1 + x 2 i {\displaystyle F_{i}=1+x^{2^{i}}} とする。すると次のようになる。 N 1 − x = N ⋅ ( 1 + x ) 1 − x 2 = N ⋅ ( 1 + x ) ⋅ ( 1 + x 2 ) 1 − x 4 = N ⋅ ( 1 + x ) ⋅ ( 1 + x 2 ) ⋅ ( 1 + x 4 ) 1 − x 8 {\displaystyle {\frac {N}{1-x}}={\frac {N\cdot (1+x)}{1-x^{2}}}={\frac {N\cdot (1+x)\cdot (1+x^{2})}{1-x^{4}}}={\frac {N\cdot (1+x)\cdot (1+x^{2})\cdot (1+x^{4})}{1-x^{8}}}} x ∈ [ 0 , 1 2 ) {\displaystyle x\in [0,{\tfrac {1}{2}})} なので、 n {\displaystyle n} ステップ後には 1 − x 2 n {\displaystyle 1-x^{2^{n}}} と 1 の相対誤差は 2 − n {\displaystyle 2^{-n}} となり、 2 n {\displaystyle 2^{n}} の二進数の精度では 1 と見なせるようになる。このアルゴリズムをIBM方式と呼ぶこともある。
※この「二項定理」の解説は、「除算 (デジタル)」の解説の一部です。
「二項定理」を含む「除算 (デジタル)」の記事については、「除算 (デジタル)」の概要を参照ください。
「二項定理」の例文・使い方・用例・文例
二項定理と同じ種類の言葉
固有名詞の分類
- 二項定理のページへのリンク
