にこう‐ぶんぷ〔ニカウ‐〕【二項分布】
二項分布
【英】: binomial distribution
1 回の試行においてある事象が起こる確率が p であるとき、この試行が互いに独立に n 回繰り返される場合に、その事象が i 回起こる確率 P(i) は下式で計算され、その値を i = 0 、1 、2 、……、n について展開した確率分布を二項分布という。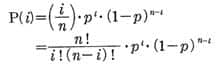 ここに、i! は i の階乗 [i×(i-1)×(i-2)×……×2×1] である。今かりに試掘の成功確率が一定で p = 0.2 と仮定し、また何回もの試掘の結果は互いに影響を与えず独立であるとすると、n 回の試掘をして i 坑が成功する確率は表のとおりである。これによれば、最も確率が高いのは、i = 0.2n の場合であるのは当然であるが、一方、試掘数nが小さいときには全く成功しない(i=0)確率もかなりあることがわかる 表 二項分布
|
|||||||||||||||||||||
2項分布
にこうぶんぷと同じ種類の言葉
- にこうぶんぷのページへのリンク
 と
と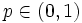 を
を の値をとる
の値をとる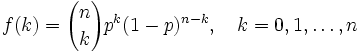
 , 裏が出る
, 裏が出る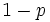 の
の