ウィーナー‐かてい〔‐クワテイ〕【ウィーナー過程】
ウィーナー過程
ウィーナー過程
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/02/21 06:13 UTC 版)

概要
ウィーナー過程は確率過程の一種であり、レヴィ過程の代表例である。連続時間マルチンゲールの研究から生じ、様々な確率過程の基礎となる確率過程である。確率解析、拡散過程、ポテンシャル論においても重要な役割を果たす。
ウィーナー過程は応用数学、物理学、計算機科学、経済学などにもしばしば現れる(⇒ #応用)。
特徴づけ
ウィーナー過程 Wt は次の条件
によって特徴付けられる。ここで、N(μ, σ2) は期待値 μ, 分散 σ2 の正規分布を表す。 また独立増分とは、「0 ≤ s ≤ t ≤ s′ ≤ t′ であるならば、Wt − Ws と Wt′ − Ws′ とが独立な確率変数となる」ことを意味する。
レヴィ条件 (Lévy characterization) からウィーナー過程を特徴づけられる。この場合、ウィーナー過程は、ほとんど確実に連続なマルチンゲールで W0 = 0 かつ二次変分 [Wt, Wt] が t になるものとして特徴づけられる。
また、係数が標準正規分布 N(0, 1) に従う独立な確率変数であるような正弦級数で表されるスペクトル表現を持つ確率過程としてウィーナー過程を特徴付ける方法もある。このような表現はカルーネン-レーヴェの定理を用いることで得られる。
平均 0, 分散 1 の独立同分布な離散時間連鎖のスケーリングの極限は、ウィーナー過程に確率収束する(ドンスカーの定理)。酔歩と同様にウィーナー過程は、一次元または二次元において再帰的 (recurrent) (つまり、出発点の半径任意の近傍に確率 1 で無限回戻ってくる)となるが、三次元以上では過渡的である。酔歩と異なる点は、それがスケール不変であることである。つまりいかなる非零定数 α ≠ 0 についても

ウィーナー過程は様々な分野で応用される。以下はその一例である:
ウィーナー過程と同じ種類の言葉
- ウィーナー過程のページへのリンク
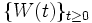 .
.  は
は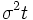 の
の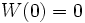 かつ
かつ 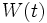 は
は 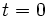 で
で
