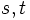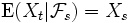マルチンゲール
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2024/09/23 08:14 UTC 版)

|
この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 (2013年1月)
|
マルチンゲール(英語: martingale)とは、確率論において、確率過程の性質の一つであり、過去の情報に制限して計算した期待値と未来の期待値が同一になる性質である。 この性質は公平な賭け事を行っているときの持ち金の変遷に現れるものだと考えられており、マルチンゲールという名前も賭けにおける戦略(マルチンゲール法[1])からとられたものである。
数学的には、情報というのは情報増大系{Ft}であたえられ、未来における期待値はこの情報による条件付期待値となる。
数学的定義
定義は連続時間の場合と離散時間の場合で多少異なっている。
連続時間マルチンゲールの定義
時刻の集合はT= [0, ∞) とし、情報増大系{Ft}t ∈ Tが与えられたとき、 実数値連続時間確率過程 Xt, t ∈ T がマルチンゲールであるとは
- 任意の時刻 t について Xt は Ft可測
- 任意の時刻 t について Xt は可積分
- 任意の時刻 t > s について E[Xt|Fs]=Xs
が成立することである。
離散時間マルチンゲールの定義
時刻の集合はT= {1,2,3,…} とし、情報増大系{Fn}n ∈ Tが与えられたとき、 実数値離散時間確率過程 Xn, n ∈ T がマルチンゲールであるとは
- 任意の時刻 n について Xn は Fn可測
- 任意の時刻 n について Xn は可積分
- 任意の時刻 n について E[Xn+1|Fn]=Xn
が成立することである。
定義において、最初の要請は Xt が Ft より多くの情報を与えないために必要であり、二番目の要請は条件付期待値が定義できるために必要であり、三番目の要請でこの確率過程が公平な賭けであることを特徴付けている。
例
離散時間マルチンゲールの例を挙げる。偏りのないコインを投げ続けたときの n 回目の結果を Xn と書くことにする。ただし、コインが表の場合は 1 で裏の場合は -1 と定める。 情報増大系については、この X 以外に情報を与えるものはないとする。すなわち Fn を
- マルチンゲールのページへのリンク
 を
を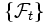 を
を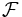 の
の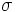 --
--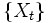 が,
が, 
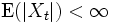 を
を