ラプラス変換
ラプラス変換
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/03/05 17:37 UTC 版)

|
この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 (2022年12月)
|

関数解析学において、ラプラス変換(ラプラスへんかん、英: Laplace transform)とは、積分で定義される関数空間の間の写像(線型作用素)の一種。関数変換。積分変換の一種。
ラプラス変換の名は18世紀の数学者ピエール=シモン・ラプラスにちなむ。
ラプラス変換によりある種の微分・積分は積などの代数的な演算に置き換わるため、制御工学などにおいて時間領域の(とくに超越的な)関数を別の領域の(おもに代数的な)関数に変換することにより、計算方法の見通しを良くするための数学的な道具として用いられる。従って、数学の中ではかなり応用寄りの分野である。
フーリエ変換を発展させて、より適用範囲を広げた計算手法である。1899年に電気技師であったオリヴァー・ヘヴィサイドが回路方程式を解くための実用的な演算子を経験則として考案して発表し、後に数学者がその演算子に対し厳密に理論的な裏付けを行った経緯がある。理論的な根拠が曖昧なままで発表されたため、この計算手法に対する懐疑的な声も多かった。この「ヘヴィサイドの演算子」の発表の後に、多くの数学者達により数学的な基盤は1780年の数学者ピエール=シモン・ラプラスの著作にある事が指摘された(この著作においてラプラス変換の公式が頻繁に現れていた)。
フーリエ変換がL^1((-∞,∞))上のゲルファント変換であるのに対しラプラス変換はL^1((0,∞))上のゲルファント変換と説明できる。
これと類似の解法として、より数学的な側面から作られた演算子法がある。こちらは演算子の記号を多項式に見立て、代数的に変形し、公式に基づいて特解を求める方法である。
定義
実数 t ≥ 0 について定義された関数 f (t) のラプラス変換とは
ラプラス変換
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2019/01/02 21:12 UTC 版)
ランプ関数の片側ラプラス変換は次の通りとなる。 L { R ( x ) } ( s ) = ∫ 0 ∞ e − s x R ( x ) d x = 1 s 2 . {\displaystyle {\mathcal {L}}\left\{R\left(x\right)\right\}(s)=\int _{0}^{\infty }e^{-sx}R(x)dx={\frac {1}{s^{2}}}.}
※この「ラプラス変換」の解説は、「ランプ関数」の解説の一部です。
「ラプラス変換」を含む「ランプ関数」の記事については、「ランプ関数」の概要を参照ください。
- ラプラス変換のページへのリンク
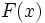
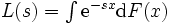 によって
によって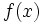 をもつ
をもつ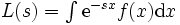 と表すことができて, このとき
と表すことができて, このとき 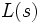 を
を 
