マルコフ連鎖の数値解法
【英】:numerical method for Markov chain
概要
マルコフ連鎖の定常分布や過渡的分布を数値的に計算するための方法. 定常分布の計算は線形方程式系を解く問題に帰着され, 解法として消去法や状態縮約法などの直接法, ヤコビ法, ガウス・ザイデル法, 状態縮約/非縮約法などの反復法がある. また, 構造化されたマルコフ連鎖に対しては行列幾何形式解を利用する方法も有力である. 一方, 過渡的分布に対しては, 離散時間ではべき乗法, 連続時間ではランダム化を利用する方法などがある.
詳説
マルコフ連鎖をマルコフ連鎖の数値的に解析する際の中心的な対象は定常分布である. 有限状態空間 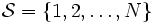 上の既約で非周期的な (つまりエルゴード的) マルコフ連鎖を考え, その推移確率行列を
上の既約で非周期的な (つまりエルゴード的) マルコフ連鎖を考え, その推移確率行列を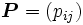 , 定常分布を
, 定常分布を 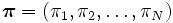 とする. 一様化により, 連続時間マルコフ連鎖の定常分布は, 離散時間マルコフ連鎖の定常分布として計算できるので, 以下では離散時間マルコフ連鎖に限定して考える.
とする. 一様化により, 連続時間マルコフ連鎖の定常分布は, 離散時間マルコフ連鎖の定常分布として計算できるので, 以下では離散時間マルコフ連鎖に限定して考える.
| (平衡方程式) | 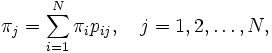 |
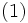 |
| (正規化条件) | 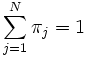 |
 |
を満たす一意の解として与えられる (式(1)) の解は定数倍に関して一意でないため, 式 (2) で正規化する). したがって, 定常分布の計算は, 原理的には線形方程式系を数値的に解く問題に帰着される. 状態数  が大きくなければ, 消去法や状態縮約法などの直接法 (反復計算を伴わない方法) でも解を求めることは可能だが, 一般にマルコフ連鎖によるモデル化はモデルが複雑になるに従って状態数が急激に増加する傾向があるため, そのような場合は計算精度などを考慮して反復法を用いることが多い.
が大きくなければ, 消去法や状態縮約法などの直接法 (反復計算を伴わない方法) でも解を求めることは可能だが, 一般にマルコフ連鎖によるモデル化はモデルが複雑になるに従って状態数が急激に増加する傾向があるため, そのような場合は計算精度などを考慮して反復法を用いることが多い.
ガウス・ザイデル法 反復法では, 反復回数 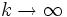 のときに定常分布
のときに定常分布 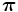 に収束するような近似値の列
に収束するような近似値の列 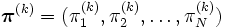 を構成する. 例えば, ヤコビ法 (Jacobi method) では, 適当な初期分布
を構成する. 例えば, ヤコビ法 (Jacobi method) では, 適当な初期分布 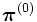 からスタートして
からスタートして
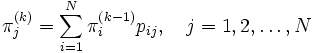
によって分布列 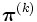 を構成し,
を構成し, 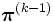 と
と 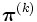 が十分近くなった時点で収束したと判断する. エルゴード的なマルコフ連鎖に対しては, ヤコビ法は計算誤差を除けば必ず収束するが, 一般に大きな
が十分近くなった時点で収束したと判断する. エルゴード的なマルコフ連鎖に対しては, ヤコビ法は計算誤差を除けば必ず収束するが, 一般に大きな  に対してはあまり収束は速くない. これに対して, ガウス・ザイデル法 (Gauss-Seidel method) では
に対してはあまり収束は速くない. これに対して, ガウス・ザイデル法 (Gauss-Seidel method) では
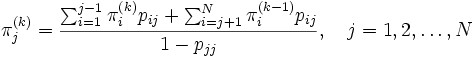
によって分布列を構成する. この方法では,  回目の反復で既に更新されている値を逐次利用するため, ヤコビ反復法に比べると一般に収束が速くなることが多い. また, 推移確率行列がブロック構造を持つ場合には, ブロックごとに更新された値を利用するブロックガウス・ザイデル法 (block Gauss-Seidel method) も有効である. さらに収束を加速する手段として過剰緩和法 (overrelaxation method) の利用がある. 過剰緩和法では, 緩和 (または加速) 係数を
回目の反復で既に更新されている値を逐次利用するため, ヤコビ反復法に比べると一般に収束が速くなることが多い. また, 推移確率行列がブロック構造を持つ場合には, ブロックごとに更新された値を利用するブロックガウス・ザイデル法 (block Gauss-Seidel method) も有効である. さらに収束を加速する手段として過剰緩和法 (overrelaxation method) の利用がある. 過剰緩和法では, 緩和 (または加速) 係数を  として
として
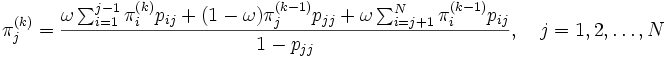
によって 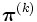 を計算する.
を計算する.  のときには, 外挿により
のときには, 外挿により 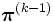 から
から 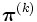 を計算しており, 適切な
を計算しており, 適切な  を選ぶことで収束を加速することが可能となる. なお, ガウス・ザイデル系の方法では, 初期分布
を選ぶことで収束を加速することが可能となる. なお, ガウス・ザイデル系の方法では, 初期分布 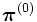 が (2) を満たしていても, 途中の計算でこの制約が満たされなくなるため, 計算の最後に (2) が満たされるよう正規化することが必要である.
が (2) を満たしていても, 途中の計算でこの制約が満たされなくなるため, 計算の最後に (2) が満たされるよう正規化することが必要である.
状態縮約/非縮約法 一方, 複数の状態をまとめて1つの状態と見なした状態数の少ない確率過程に対して反復計算を行う方法に状態縮約/非縮約法 (aggregation/disaggregation method: AD法) がある. 例えば, 状態空間を 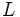 個の部分空間
個の部分空間  に分割し,
に分割し, 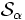 には
には 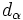 個の状態
個の状態 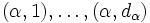 が含まれる場合を考え, 推移確率を
が含まれる場合を考え, 推移確率を 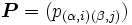 , 状態
, 状態 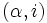 の定常確率を
の定常確率を 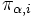 , 部分空間
, 部分空間 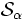 の定常確率を
の定常確率を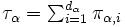 とする. いま,
とする. いま, 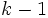 回の反復で近似値
回の反復で近似値 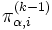 ,
, 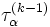 が求められているとしよう.
が求められているとしよう.  回目の反復計算のうち, まず縮約フェーズでは, 部分空間
回目の反復計算のうち, まず縮約フェーズでは, 部分空間 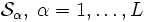 をそれぞれ1つの状態
をそれぞれ1つの状態 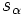 に縮約した
に縮約した 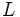 状態の確率過程を考え, それをマルコフ連鎖と見なして (特殊なケースを除いて縮約した確率過程はマルコフ連鎖とならない) 推移確率, 例えば
状態の確率過程を考え, それをマルコフ連鎖と見なして (特殊なケースを除いて縮約した確率過程はマルコフ連鎖とならない) 推移確率, 例えば 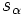 から
から 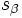 への推移確率を
への推移確率を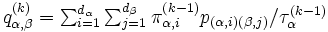 によって定める. このマルコフ連鎖
によって定める. このマルコフ連鎖 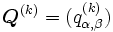 の平衡方程式を解いて, 更新された定常確率
の平衡方程式を解いて, 更新された定常確率 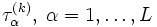 を求める. 次に非縮約フェーズでは, 1つの着目した部分空間はそのままで他のすべての部分空間を1つの状態に縮約した確率過程を近似的にマルコフ連鎖と考える. 例えば, 部分空間
を求める. 次に非縮約フェーズでは, 1つの着目した部分空間はそのままで他のすべての部分空間を1つの状態に縮約した確率過程を近似的にマルコフ連鎖と考える. 例えば, 部分空間 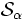 に注目した場合には,
に注目した場合には, 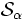 内の推移確率は元のままで,
内の推移確率は元のままで, 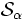 内の状態
内の状態 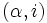 から縮約された状態への推移確率は
から縮約された状態への推移確率は 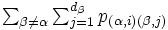 , 逆に縮約された状態から
, 逆に縮約された状態から 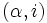 への推移確率は
への推移確率は 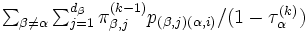 で与えられるマルコフ連鎖を考え, その定常分布を計算し
で与えられるマルコフ連鎖を考え, その定常分布を計算し 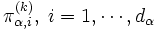 を得る. この計算を, 注目する部分空間を
を得る. この計算を, 注目する部分空間を 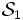 から
から 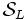 まで変えながら行えば, 更新された定常確率を求めることができる. この縮約/非縮約の手続きを, 値が収束するまで反復すればよい.
まで変えながら行えば, 更新された定常確率を求めることができる. この縮約/非縮約の手続きを, 値が収束するまで反復すればよい.
無限状態と過渡的分布 状態数が無限のマルコフ連鎖に対しては, 状態空間を適当な有限サイズで打ち切って数値計算を行うが, 打ち切るサイズによって計算時間と計算精度の間にトレードオフが生じるので注意が必要である. 構造が入っている場合 (後述) は, 上の方法を用いるにしてもその構造をうまく利用することによって, 少ない計算量で精度良い解が計算できることが多い.
定常分布に比べると, 過渡的分布 (各時点における推移確率) の計算方法はそれほど多くないが, 離散時間マルコフ連鎖に対してはべき乗法, 連続時間マルコフ連鎖に対してはランダム化を利用する方法などが知られている.
構造化されたマルコフ連鎖 確率モデル, 特に待ち行列モデルから派生するマルコフ連鎖には, 何らかの構造を持つものが多いため, その構造を利用した数値計算法が開発されている. 代表例として, 相型待ち行列に対する行列幾何形式解を考えよう. 到着過程やサービス過程}にマルコフ型到着過程や相型分布を導入することで, 広い範囲の待ち行列モデルは準出生死滅過程 (quasi-birth-and-death process) を含むGI/M/1型, あるいはM/G/1型マルコフ過程などの構造化されたマルコフ連鎖で表現することができる. このうち, GI/M/1型マルコフ連鎖は, レベル 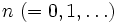 と相
と相 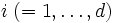 の組
の組 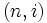 によって状態が表されるマルコフ連鎖で, 1回の推移では高々1つ上のレベルまでしか推移せず, またレベル
によって状態が表されるマルコフ連鎖で, 1回の推移では高々1つ上のレベルまでしか推移せず, またレベル  の状態からレベル
の状態からレベル 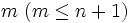 の状態への推移確率 (または推移速度) がレベルの差
の状態への推移確率 (または推移速度) がレベルの差 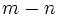 と各状態の相によって決まる性質を持っている. レベル
と各状態の相によって決まる性質を持っている. レベル  の状態の定常確率ベクトルを
の状態の定常確率ベクトルを 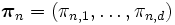 で表すと, 行列幾何形式解より, 公比行列
で表すと, 行列幾何形式解より, 公比行列 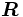 を用いて
を用いて

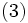
と表される. 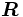 は推移確率行列の要素を係数とする非線形行列方程式の非負最小解として与えられ, 逐次代入法などで計算することができる. また
は推移確率行列の要素を係数とする非線形行列方程式の非負最小解として与えられ, 逐次代入法などで計算することができる. また 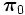 は境界条件に相当する線形方程式を解いて求められる [2]. この方法は, 本来無限次元の定常分布を有限次元のベクトルと行列で表せるという特徴を持つが, 高速化のためには
は境界条件に相当する線形方程式を解いて求められる [2]. この方法は, 本来無限次元の定常分布を有限次元のベクトルと行列で表せるという特徴を持つが, 高速化のためには 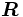 の計算方法がポイントとなる.
の計算方法がポイントとなる.
なお, M/G/1型マルコフ連鎖は行列幾何形式解を持たないが, やはりその構造を利用したさまざまな方法が考えられている [2].
[1] D. P. Heyman and M. J. Sobel (eds.), 伊理, 今野, 刀根監訳, 『確率モデルハンドブック』, 朝倉書店, 1995.
[2] M. F. Neuts, Matrix Goemtric Solutions in Stochastic Models - An Algorithmic Approach, Johns Hopkins Univ. Press, 1981.
[3] M. F. Neuts, Structured Stochastic Matrices of {rm M/G/1} Type and Their Applications, Marcel Dekker, 1989.
[4] W. J. Stewart (ed.), Numerical Solution of Markov Chains, Marcel Dekker, 1991.
[5] W. K. Grassmann (ed.), Computational Probability, Kluwer Academic Publishers, 2000.
- マルコフ連鎖の数値解法のページへのリンク
