マルコフ‐れんさ【マルコフ連鎖】
マルコフ連鎖
【英】:Markov chain
概要
マルコフ性をもつ離散状態空間上の確率過程. すなわち, 確率過程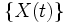 が, 任意の
が, 任意の と
と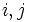 に対して
に対して
 |  |
 |
詳説
マルコフ過程 独立性を緩めた性質であるマルコフ性を持つ確率過程のことをマルコフ過程と呼び, その中で状態が離散的なものを一般にマルコフ連鎖と呼ぶ. マルコフ連鎖は最も基本的で応用範囲の広い\確率過程の一つである.
離散時間マルコフ連鎖 離散的な状態空間 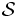 上の確率過程
上の確率過程  が, 任意の時点
が, 任意の時点  ,
, 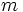 と任意の状態
と任意の状態  に対して
に対して

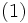
を満たすとき, 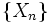 を離散時間マルコフ連鎖と呼ぶ. (1) は, 将来の分布が現在の状態のみで定まり, 過去の状態には依存しない性質を表しており, マルコフ性と呼ばれる.賭けの問題における所持金の推移や, 在庫理論における各期の在庫量の変化など, マルコフ性を持つと考えられる例は多い.
を離散時間マルコフ連鎖と呼ぶ. (1) は, 将来の分布が現在の状態のみで定まり, 過去の状態には依存しない性質を表しており, マルコフ性と呼ばれる.賭けの問題における所持金の推移や, 在庫理論における各期の在庫量の変化など, マルコフ性を持つと考えられる例は多い.
(1) の推移確率が, 時点 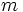 に依存しない場合, マルコフ連鎖は斉時的であるという. 斉時的な離散時間マルコフ連鎖
に依存しない場合, マルコフ連鎖は斉時的であるという. 斉時的な離散時間マルコフ連鎖 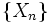 に対して,
に対して,  を
を  ステップ推移確率,
ステップ推移確率,  を
を  ステップ推移確率行列と呼ぶ. 特に 1ステップ推移確率を
ステップ推移確率行列と呼ぶ. 特に 1ステップ推移確率を  で表し,
で表し,  を推移確率行列と呼ぶ. チャップマン・コルモゴロフの等式 (Chapman-Kolmogorov equation)
を推移確率行列と呼ぶ. チャップマン・コルモゴロフの等式 (Chapman-Kolmogorov equation)  から
から  が成り立つので, 1 ステップ推移確率行列
が成り立つので, 1 ステップ推移確率行列  が与えられれば, 任意のステップの推移確率を計算することができる.
が与えられれば, 任意のステップの推移確率を計算することができる.
既約なマルコフ連鎖と吸収的マルコフ連鎖 状態の組 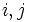 に対して, 適当な
に対して, 適当な  で
で  となる場合,
となる場合,  から
から 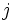 へ到達可能であるという. 任意の状態から他のどの状態へも到達可能であるマルコフ連鎖は既約であるという. 一方,
へ到達可能であるという. 任意の状態から他のどの状態へも到達可能であるマルコフ連鎖は既約であるという. 一方,  である状態
である状態  は, 一度入ると他の状態へ推移できないため吸収状態と呼ばれる. 任意の状態から出発したとき確率1でいつかはいずれかの吸収状態に到達するマルコフ連鎖を吸収的という. 後述するように, 既約なマルコフ連鎖では長期間観察したときに各状態に滞在する時間の割合が主な分析対象となる. これに対し, 吸収的マルコフ連鎖では, 吸収されるまでの挙動, 例えば吸収時間の分布, 吸収までに各状態に滞在する平均ステップ数, 複数の吸収状態がある場合に各状態への吸収確率, などが分析の対象となる.
は, 一度入ると他の状態へ推移できないため吸収状態と呼ばれる. 任意の状態から出発したとき確率1でいつかはいずれかの吸収状態に到達するマルコフ連鎖を吸収的という. 後述するように, 既約なマルコフ連鎖では長期間観察したときに各状態に滞在する時間の割合が主な分析対象となる. これに対し, 吸収的マルコフ連鎖では, 吸収されるまでの挙動, 例えば吸収時間の分布, 吸収までに各状態に滞在する平均ステップ数, 複数の吸収状態がある場合に各状態への吸収確率, などが分析の対象となる.
 となるすべての
となるすべての 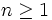 の最大公約数を, 状態
の最大公約数を, 状態  の周期と定める. 既約なマルコフ連鎖では, すべての状態は同じ周期を持つことが知られている. また, 周期 1 のマルコフ連鎖を非周期的という.
の周期と定める. 既約なマルコフ連鎖では, すべての状態は同じ周期を持つことが知られている. また, 周期 1 のマルコフ連鎖を非周期的という.
 から
から 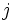 への初到達時間を
への初到達時間を 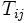 とすると, マルコフ連鎖の各状態 (
とすると, マルコフ連鎖の各状態 ( とする) はその状態への再帰確率
とする) はその状態への再帰確率  と平均再帰時間
と平均再帰時間  により以下のように分類される.
により以下のように分類される.
 | 一時的  | ||
再帰的  |  | 零再帰的  | |
正再帰的  |
なお, 既約なマルコフ連鎖ではすべての状態は同じ分類に属するので, これらはマルコフ連鎖自身の分類でもある. 特に, 既約で非周期的かつ正再帰的なマルコフ連鎖は, エルゴード的マルコフ連鎖と呼ばれる.
定常分布  のとき
のとき  が初期状態
が初期状態  に無関係な正定数
に無関係な正定数  に収束し, 正規化条件
に収束し, 正規化条件  を満たす場合,
を満たす場合,  を極限分布と呼ぶ. 極限分布は平衡方程式
を極限分布と呼ぶ. 極限分布は平衡方程式  を満たすため, この方程式と正規化条件から求めることができる. 極限分布に対して, 平衡方程式を満たす確率分布を定常分布と呼ぶ. 極限分布は定常分布であるが, 周期的なマルコフ連鎖のように定常分布は必ずしも極限分布とならない. 既約で非周期的なマルコフ連鎖に対しては, (1) 正再帰的であること, (2) 極限分布が存在すること, (3) 平衡方程式と正規化条件が一意の解を持つこと, の3条件は同値となる. 実際, エルゴード的なマルコフ連鎖では
を満たすため, この方程式と正規化条件から求めることができる. 極限分布に対して, 平衡方程式を満たす確率分布を定常分布と呼ぶ. 極限分布は定常分布であるが, 周期的なマルコフ連鎖のように定常分布は必ずしも極限分布とならない. 既約で非周期的なマルコフ連鎖に対しては, (1) 正再帰的であること, (2) 極限分布が存在すること, (3) 平衡方程式と正規化条件が一意の解を持つこと, の3条件は同値となる. 実際, エルゴード的なマルコフ連鎖では  となり, 極限分布は
となり, 極限分布は 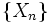 を長時間観測したときに各状態に滞在する時間の割合に一致する. なお, 有限状態のマルコフ連鎖が既約で非周期的であれば, 必ず正再帰的となる. 一方, 状態
を長時間観測したときに各状態に滞在する時間の割合に一致する. なお, 有限状態のマルコフ連鎖が既約で非周期的であれば, 必ず正再帰的となる. 一方, 状態 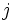 が一時的もしくは零再帰的ならば,
が一時的もしくは零再帰的ならば,  となり極限分布は存在しない.
となり極限分布は存在しない.
連続時間マルコフ連鎖 離散状態空間上の連続時間確率過程  が, 任意の時点
が, 任意の時点 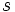 ,
, 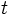 と状態
と状態 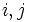 , および履歴
, および履歴  に対して
に対して

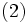
を満たすとき, 連続時間マルコフ連鎖と呼ぶ. ポアソン過程や出生死滅過程などは, 代表的な連続時間マルコフ連鎖である.
離散時間の場合と同様に, (2) が 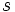 に依存しないマルコフ連鎖を斉時的といい, 推移確率を
に依存しないマルコフ連鎖を斉時的といい, 推移確率を  , 推移確率行列を
, 推移確率行列を  で表す. 異なる状態
で表す. 異なる状態 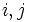 に対して,
に対して,  を状態
を状態  から
から 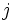 への推移速度といい,
への推移速度といい,  を非対角要素, 対角要素を
を非対角要素, 対角要素を  とする行列
とする行列 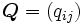 を推移速度行列と呼ぶ. マルコフ性から, 連続時間マルコフ連鎖が状態
を推移速度行列と呼ぶ. マルコフ性から, 連続時間マルコフ連鎖が状態  に滞在する時間はパラメータ
に滞在する時間はパラメータ  の指数分布に従う. また,
の指数分布に従う. また,  は状態
は状態  での滞在が終了したという条件の下で, 推移先が
での滞在が終了したという条件の下で, 推移先が 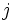 である条件付き確率を与える. 推移速度行列
である条件付き確率を与える. 推移速度行列 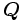 が与えられると, 推移確率はコルモゴロフの後退方程式
が与えられると, 推移確率はコルモゴロフの後退方程式  , あるいはコルモゴロフの前進方程式
, あるいはコルモゴロフの前進方程式  によって特徴付けられる. この関係から, 応用上現れる多くのマルコフ連鎖では推移確率が
によって特徴付けられる. この関係から, 応用上現れる多くのマルコフ連鎖では推移確率が で表される.
で表される.
離散時間マルコフ連鎖と同様に, 任意の状態から他のどの状態へも推移可能な場合, このマルコフ連鎖は既約であるという. また, 状態の分類 (一時的, 零再帰的, 正再帰的) も, 各状態への再帰時間  の性質により離散時間マルコフ連鎖の場合と同様に定義される. 極限分布についても, 初期状態
の性質により離散時間マルコフ連鎖の場合と同様に定義される. 極限分布についても, 初期状態  に無関係に
に無関係に  と収束し,
と収束し,  が成り立つ場合,
が成り立つ場合,  を極限分布とよぶ. 極限分布は, 平衡方程式
を極限分布とよぶ. 極限分布は, 平衡方程式  と正規化条件
と正規化条件  から求めることができる. 既約な連続時間マルコフ連鎖に対しては, 正再帰的であること, 極限分布が存在すること, 平衡方程式と正規化条件を満たす
から求めることができる. 既約な連続時間マルコフ連鎖に対しては, 正再帰的であること, 極限分布が存在すること, 平衡方程式と正規化条件を満たす  が存在すること, の3条件は同値である.
が存在すること, の3条件は同値である.
マルコフ連鎖の一般化 マルコフ性は独立性を少し緩めた概念だが, 適用範囲は広い. 例えば, 離散時間確率過程 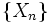 の将来の時点における分布が, 現在の状態
の将来の時点における分布が, 現在の状態 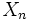 と過去の
と過去の 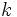 状態
状態  に依存する場合,
に依存する場合, 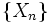 自身はマルコフ連鎖とならないが,
自身はマルコフ連鎖とならないが,  はマルコフ連鎖となる. また, 状態の推移はマルコフ連鎖に従い, 各状態の滞在時間分布が一般分布に拡張された確率過程はセミマルコフ過程と呼ばれ, マルコフ連鎖による分析が援用できる.さらに, そのままではマルコフ性を持たない確率過程に対しても, 隠れマルコフ連鎖法や補助変数法を利用することでマルコフ連鎖としてモデル化できる場合が少なくない. このようなモデル化における汎用性・柔軟性は, マルコフ連鎖が広く利用される大きな理由となっている.
はマルコフ連鎖となる. また, 状態の推移はマルコフ連鎖に従い, 各状態の滞在時間分布が一般分布に拡張された確率過程はセミマルコフ過程と呼ばれ, マルコフ連鎖による分析が援用できる.さらに, そのままではマルコフ性を持たない確率過程に対しても, 隠れマルコフ連鎖法や補助変数法を利用することでマルコフ連鎖としてモデル化できる場合が少なくない. このようなモデル化における汎用性・柔軟性は, マルコフ連鎖が広く利用される大きな理由となっている.
[1] K. L. Chang, Markov Chains with Stationary Transition Probabilities, Springer-Verlag, 1967.
[2] D. Freedman, Markov Chains, Springer, 1983.
[3] J. G. Kemenny and J. L. Snell, Finite Markov Chain, Van Nostrand, 1960.
マルコフ連鎖
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2023/06/27 14:32 UTC 版)
マルコフ連鎖(マルコフれんさ、英: Markov chain)とは、確率過程の一種であるマルコフ過程のうち、とりうる状態が離散的(有限または可算)なもの(離散状態マルコフ過程)をいう。また特に、時間が離散的なもの(時刻は添え字で表される)を指すことが多い[注釈 1]。マルコフ連鎖は、未来の挙動が現在の値だけで決定され、過去の挙動と無関係である(マルコフ性)。各時刻において起こる状態変化(遷移または推移)に関して、マルコフ連鎖は遷移確率が過去の状態によらず、現在の状態のみによる系列である。特に重要な確率過程として、様々な分野に応用される。
- ^ 他に連続時間マルコフ過程というものもあり、これは時刻が連続である。
「マルコフ連鎖」の例文・使い方・用例・文例
- マルコフ連鎖のページへのリンク

