ポアソン‐かてい〔‐クワテイ〕【ポアソン過程】
ポアソン過程
【英】:Poisson process
概要
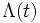 を連続な非減少実数値関数とする. 計数過程
を連続な非減少実数値関数とする. 計数過程 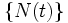 が平均測度
が平均測度 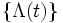 をもつ
(非定常)ポアソン過程であるとは次を満たすことである.
をもつ
(非定常)ポアソン過程であるとは次を満たすことである.
(1) 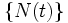 は独立増分をもつ.
は独立増分をもつ.
(2) 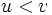 に対し
に対し 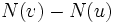 は平均
は平均 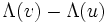 のポアソン分布にしたがう.
のポアソン分布にしたがう.
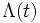 が微分可能なときは
が微分可能なときは 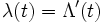 が
が 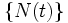 の強度となる. 特に,
の強度となる. 特に, 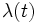 が定数のときは定常ポアソン過程である.
が定数のときは定常ポアソン過程である.
詳説
ポアソン過程 (Poisson process) は, ランダムに生起する事象を表す基本的な確率過程で, 客の到着や故障の発生, 個体の出生など様々な現象のモデル化に使われる. 一方, 出生死滅過程は個体の出生だけでなくランダムな死滅も考慮した確率過程で, 待ち行列理論をはじめ広く利用されている.
ポアソン過程 事象の生起時点列を 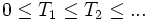 とし,
とし, 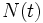 を区間
を区間 ![[0, t]\,](https://cdn.weblio.jp/e7/img/dict/orjtn/d4d8c7a80120c102d35067b23525fcec.png) における事象の生起数,
における事象の生起数, 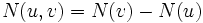 を区間
を区間 ![(u, v]\,](https://cdn.weblio.jp/e7/img/dict/orjtn/6de2e3bc1b1d527addb328985aae3b6d.png) での生起数とする. このような確率過程
での生起数とする. このような確率過程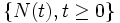 は一般に計数過程と呼ばれる. 計数過程
は一般に計数過程と呼ばれる. 計数過程 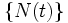 がポアソン過程であるとは, 正の実数
がポアソン過程であるとは, 正の実数 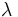 が存在して任意の
が存在して任意の 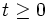 および
および 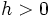 に対して
に対して
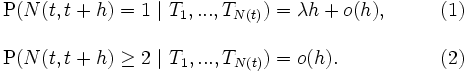
が成り立つことである.
(1), (2) はランダムな事象の生起を3つの点で特徴付けている. 第1は, 微小区間 ![(t, t+h]\,](https://cdn.weblio.jp/e7/img/dict/orjtn/a71ff74a88dbd6e7628a876bdfa06629.png) に事象が生起する確率は時刻
に事象が生起する確率は時刻  以前の挙動に独立であるという点, 第2は, 微小区間に2つ以上の事象が生起する確率は無視できるという点, 第3は, 微小区間に事象の生起する確率が時刻によらない点である. 式 (1) の
以前の挙動に独立であるという点, 第2は, 微小区間に2つ以上の事象が生起する確率は無視できるという点, 第3は, 微小区間に事象の生起する確率が時刻によらない点である. 式 (1) の 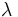 を強度 (intensity) または生起率と呼ぶ. これは単位時間あたりの平均生起数を表す. 強度を時間の関数
を強度 (intensity) または生起率と呼ぶ. これは単位時間あたりの平均生起数を表す. 強度を時間の関数 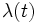 に拡張したものは非定常ポアソン過程と呼ばれる. 以下はポアソン過程の性質であり, それぞれがポアソン過程の同値な定義でもある.
に拡張したものは非定常ポアソン過程と呼ばれる. 以下はポアソン過程の性質であり, それぞれがポアソン過程の同値な定義でもある.
性質1 ポアソン過程 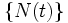 において,事象の生起間隔の列
において,事象の生起間隔の列  は互いに独立で平均
は互いに独立で平均 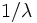 の
指数分布に従う.
\medskip
の
指数分布に従う.
\medskip
性質2 ポアソン過程 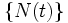 は独立増分過程で, 任意の
は独立増分過程で, 任意の 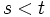 に対して
に対して 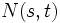 は平均
は平均 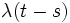 のポアソン分布に従う.
のポアソン分布に従う.
性質1は指数分布の無記憶性から自然に導かれる. また, 性質2より複数の独立なポアソン過程の重ね合わせは, それぞれの強度の和を強度に持つポアソン過程となることが分かる. また, 次の定理は確率変数の和に対する少数の法則の確率過程版である.
定理1 各  に対して
に対して 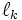 個の計数過程
個の計数過程  を考え, その重ね合わせを
を考え, その重ね合わせを 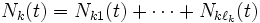 とする.
とする. 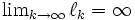 で, かつ (a)
で, かつ (a) 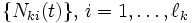 は互いに独立, (b) 任意の
は互いに独立, (b) 任意の 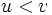 に対して
に対して 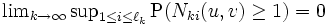 が成り立つとすると,
が成り立つとすると, 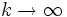 のとき
のとき  が平均測度
が平均測度 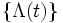 の (非定常) ポアソン過程に収束するための必要十分条件は, 任意の
の (非定常) ポアソン過程に収束するための必要十分条件は, 任意の 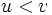 に対して,
に対して, 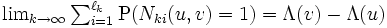 および
および 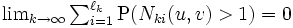 が成り立つことである. なお,
が成り立つことである. なお, 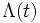 が微分可能ならば強度は
が微分可能ならば強度は 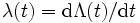 となる.
となる.
定理1は, 実際に起こる様々な現象をポアソン過程を用いて表わすことの妥当性を示唆している. 例えば, 電話網のある回線群への接続要求 (呼) は非常に多くの電話機からかかってくる呼の重ね合わせとみなせる. この場合, 各電話機は独立に使われており (仮定 (a)), その頻度は十分小さい (仮定 (b)) と考えられるため, この回線群への呼の発生はポアソン過程としてモデル化できるであろう. この他にも, マルチンゲールによるポアソン過程の特徴付けや, 事象平均と時間平均の同等性を示すPASTA (Poisson arrivals see time averages) など, ポアソン過程には興味深い性質が多い.
ポアソン過程の一般化 ポアソン過程を特徴付ける3つの条件のうち第2の条件を緩め, 事象の生起時点列はポアソン過程であるが, 各生起時点で同時に発生する事象の数は独立で同一の分布に従う確率変数である場合, 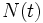 は複合ポアソン過程と呼ばれる. また, 非定常ポアソン過程の強度
は複合ポアソン過程と呼ばれる. また, 非定常ポアソン過程の強度 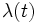 を確率過程に拡張したものは2重確率ポアソン過程 (doubly stochastic Poisson process) と呼ばれる. 例えば, マルコフ変調ポアソン過程は
を確率過程に拡張したものは2重確率ポアソン過程 (doubly stochastic Poisson process) と呼ばれる. 例えば, マルコフ変調ポアソン過程は 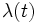 が連続時間マルコフ連鎖に従う例である.
が連続時間マルコフ連鎖に従う例である.
出生過程 性質1より, ポアソン過程は状態空間 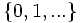 上の連続時間マルコフ連鎖であることがわかる. 推移速度行列を
上の連続時間マルコフ連鎖であることがわかる. 推移速度行列を 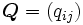 とすると, 性質1から
とすると, 性質1から 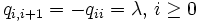 でその他の
でその他の 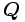 の要素は全て0となる. これを一般化して,
の要素は全て0となる. これを一般化して,  から
から  への推移速度が
への推移速度が  に依存して
に依存して 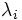 で定まるマルコフ連鎖を出生過程 (birth process)と呼ぶ. 出生過程の推移速度行列は
で定まるマルコフ連鎖を出生過程 (birth process)と呼ぶ. 出生過程の推移速度行列は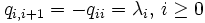 で, その他の要素は0である.
で, その他の要素は0である.
出生死滅過程 出生過程では, 状態は  から
から  というように1ずつ進んでいくが,
というように1ずつ進んでいくが,  から
から 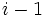 へ戻ることも許すように一般化すると,
へ戻ることも許すように一般化すると,  かつ
かつ 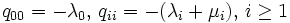 で, その他の要素は0の推移速度行列が得られる. このような3重対角の推移速度行列に従う連続時間マルコフ連鎖を出生死滅過程 (birth and death process) という. また,
で, その他の要素は0の推移速度行列が得られる. このような3重対角の推移速度行列に従う連続時間マルコフ連鎖を出生死滅過程 (birth and death process) という. また, 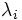 ,
, 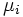 はそれぞれ状態
はそれぞれ状態  での出生率, 死滅率と呼ばれる. 出生死滅過程では, 状態
での出生率, 死滅率と呼ばれる. 出生死滅過程では, 状態 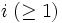 に滞在する時間の長さはパラメータ
に滞在する時間の長さはパラメータ 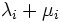 の指数分布に従い, 滞在時間を終えると確率
の指数分布に従い, 滞在時間を終えると確率 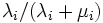 で状態
で状態  へ, 確率
へ, 確率 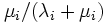 で状態
で状態 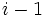 へ推移する.
へ推移する.
出生死滅過程は隣り合う状態間でのみ推移が起きるという特徴を持つため, 定常分布などの特性量が陽な形で得られる. 例えば, 応用上重要な 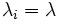 ,
, 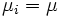 の出生死滅過程は,
の出生死滅過程は, 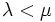 のとき正再帰的で,
のとき正再帰的で, 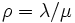 とすると状態
とすると状態  にいる定常確率は
にいる定常確率は 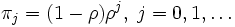 という幾何分布となる. なお,
という幾何分布となる. なお, 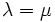 のときは零再帰的,
のときは零再帰的, 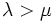 のときは一時的となり定常分布は存在しない. この例はM/M/1 待ち行列モデルに相当する出生死滅過程であるが, 出生死滅過程はより一般的なM/M/c 待ち行列モデル (M/M/
のときは一時的となり定常分布は存在しない. この例はM/M/1 待ち行列モデルに相当する出生死滅過程であるが, 出生死滅過程はより一般的なM/M/c 待ち行列モデル (M/M/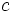 待ち行列モデル) などのマルコフ型の待ち行列モデルや, 機械修理モデルを解析する上でも重要な確率過程となっている.
待ち行列モデル) などのマルコフ型の待ち行列モデルや, 機械修理モデルを解析する上でも重要な確率過程となっている.
[1] P. Brémaud, Point Processes and Queues, Springer-Verlag, 1981.
[2] D. R. Cox and V. Isham, Point Processes, Chapman and Hall, 1980.
[3] R. W. Wolff, Stochastic Modeling and the Theory of Queues, Prentice-Hall, 1989.
ポアソン過程
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2020/12/23 16:36 UTC 版)
「オープンソースソフトウェアのセキュリティ」の記事における「ポアソン過程」の解説
ポアソン過程(英語版)はオープンソースとクローズドソースのソフトウェアの間でセキュリティ障害が発覚した割合を評価するために利用することができる。ポアソン過程において脆弱性の数をNv、有償レビュー者数をNpとする。障害を発見する無償レビュー者の割合はλv、障害を発見する有償レビュー者の割合はλpとなる。無償レビューグループが障害を発見する期待時間は1/(Nv λv)、有償レビューグループが障害を発見する期待時間は1/(Nv λv)となる。
※この「ポアソン過程」の解説は、「オープンソースソフトウェアのセキュリティ」の解説の一部です。
「ポアソン過程」を含む「オープンソースソフトウェアのセキュリティ」の記事については、「オープンソースソフトウェアのセキュリティ」の概要を参照ください。
ポアソン過程と同じ種類の言葉
- ポアソン過程のページへのリンク
