対数正規分布
【英】: lognormal distribution
同義語: 油田規模分布
確率変数の対数値が正規分布をするような統計分布を対数正規分布という。数学的には、正規分布の分布密度関数が式 (1) で表現されるのに対して、対数正規分布は式 (2) で表される分布として定義される。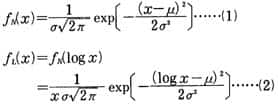 上式で μ は平均値、σ2 は分散である。対数正規分布を a) 実数座標、b) 実数対数座標、c) 対数正規確率紙を用いてグラフに表すと図のとおりである。c) の横軸の目盛りは、変数 x についての実数目盛りを x が 0 から xi までの確率累積値 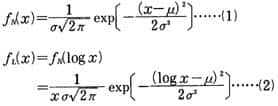 に転換した目盛りである。このグラフの上で直線になるか否かで対数正規分布であるか否かが検定できる。 に転換した目盛りである。このグラフの上で直線になるか否かで対数正規分布であるか否かが検定できる。対数正規分布は、恒星の密度、鉱物の塊粒の寸法・重量、鉱床の規模、音の強さ、材料の寿命、生物群の個体数、生物個体の寸法・重量、市町村の人口、個人所得額など、天文、地質、物理、生物、社会の各現象に広く見られる統計分布であり、石油・天然ガス鉱床においても、層厚、孔隙率{こうげきりつ}、埋蔵量の値が対数正規分布をすることが認められている。鉱床ごとの埋蔵量の分布については、この法則が一つの堆積盆地{たいせきぼんち}についても、また地理的区分についても、世界全体についても当てはまることが示されている。ただし各地区区分ごとに係数 μ 、σ が異なり、埋蔵量の平均値や分布の分散は異なる。 この対数正規分布の特色は、規模の大きい個体は数が少なく、規模の小さい例は数が多いということであり、また、それにもかかわらず大きい方からある程度の数の個体の規模を合計すると全体合計規模の大部分のシェアを占めるということである。Denver-Julesburg 盆地の例では大きい方から数えて 4.1 %の数の油田だけで全体究極可採量の 47.7 %、上から 9 %の数をとると量では 66 %を占める。このような現象は世界全体でも認められるところであり、石油探鉱・開発の経済においても大きな要素である。 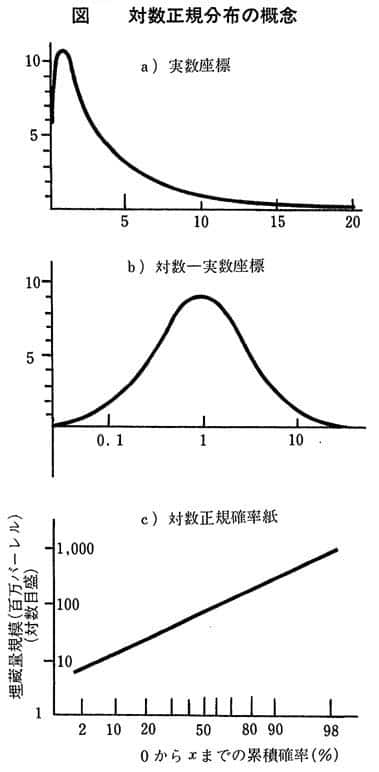 |
油田規模分布
対数正規分布 log-normal distribution
詳しくは,別のページを参照のこと。
対数正規分布
対数正規分布
対数正規分布
対数正規分布
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/12/18 05:27 UTC 版)
「ランダム・ウォーク理論」の記事における「対数正規分布」の解説
株価の変動は幾何ブラウン運動によって支配されていると仮定する。すると株価の収益率は対数正規分布に従うことが知られている。TOPIXの過去収益率データは概ね対数正規分布に従うことが知られている。
※この「対数正規分布」の解説は、「ランダム・ウォーク理論」の解説の一部です。
「対数正規分布」を含む「ランダム・ウォーク理論」の記事については、「ランダム・ウォーク理論」の概要を参照ください。
- 対数正規分布のページへのリンク
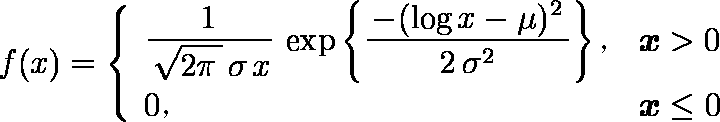
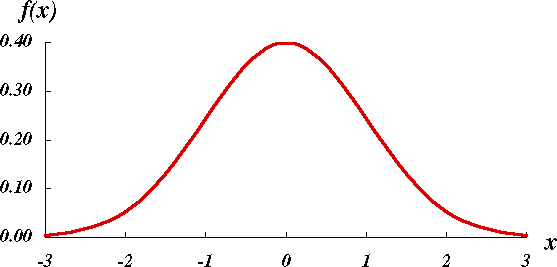
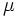 ,
,
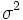 とすると,
とすると,
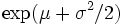 となる.
となる.


